Aplicación de la Termotecnia.
Caso práctico: vivienda solar
Esta es la primera Unidad del módulo de Equipos e Instalaciones Térmicas y en ella vamos a tratar los conceptos básicos de energía, calor, temperatura y comportamiento de los gases. Gracias a todo ello, seremos capaces de comprender los fundamientos científicos y tecnologícos de equipos e instalaciones como el de la figura, donde puedes ver un sistema integrado de calentamiento de una vivienda, mediante tecnologías activas y pasivas. La Termotecnia, estudia todo ello.

En el dibujo, puedes comprobar cómo se aprovecha en una casa la energía solar, mediante tecnologías activas (colectores solares) y arquitectura solar pasiva (geometría y propiedades de los materiales constructivos). Unos colectores térmicos solares calientan el fluido que circula por ellos (usualmente agua con anticongelante) y se almacena en un tanque que, a su vez, aprovecha esta energía térmica para alimentar un circuito en forma de serpentín que, además de calentar la vivienda, almacena el calor para las horas en las que no hay radiación solar.
También vemos que los rayos de sol en invierno forman un ángulo menor con el terreno, por lo que entra una mayor radiación solar en la vivienda que en verano, cuando el sol alcanza mayor altura y no penetra la radiación en la casa. Por lo tanto, mediante soluciones como las que se muestran, se consigue un menor consumo energético y una mayor eficiencia energética.
La sistematización de soluciones como las propuestas implica el manejar conceptos como energía, potencia térmica, comportamiento de los gases, transmitancia o inercia térmica y comprender el funcionamiento de equipos e instalaciones térmicas. De todo ello nos ocuparemos en esta y en las sucesivas unidades didácticas.
Debes conocer
Formas de energía
La energía adopta diferentes formas: mecánica, química, eléctrica, térmica, etc., y mediante distintos procedimientos y dispositivos podemos transformarla de un tipo a otro. No obstante no es lo mismo transformar calor en electricidad que a la inversa. La energía calorífica o térmica es la forma más degradada de la energía, mientras que la energía eléctrica es la más elaborada.
En la siguiente simulación puedes realizar diferentes experimentos mediante el simulador virtual. Activa el botón de inicio y calienta los distintos cuerpos y sustancias, observando lo que ocurre. Pulsa el botón de Systems y transforma distintos tipos de energía en otras formas, observa lo que ocurre.
Conducción térmica
Mediante el simulador anterior, realiza un experimento para comprobar ¿qué se calienta antes, aplicando el mismo calor, el recipiente con una determinada masa de agua o el bloque de hierro de la misma masa? Monta el experimento y justifica el resultado.
RESULTADO: En primer lugar, hay que montar el experimento de la manera que se muestra en la imagen

La explicación en la rapidez con la que se calienta el hierro, frente a la del agua, tiene dos causas. Por un lado, la conducción térmica del hierro es mayor que la del agua: el calor se transmite con mayor facilidad. A esto se le llama conductividad térmica. La otra causa es la cantidad de calor que puede acumularse por unidad de masa. Es decir, el agua es capaz de acumular en 1 kg más cantidad de energía calorífica que 1 kg de hierro, estando ambos a la misma temperatura. A ello se le denomina calor específico. Ambos conceptos, así como sus unidades de medida, se verán a lo largo de este módulo.
Transformaciones de energía
Observa la siguiente imagen, procedente del simulador anterior y señala las transformaciones energéticas que se producen y los tipos de energía implicados.

RESULTADO: Las transformaciones energéticas que se producen son las siguientes:
En primer lugar, pasando por alto la transformación energética que se origina en el Sol debido a las reacciones de fusión y que desprende energía radiante, la radiación solar llega a las placas fotovoltaicas y genera electricidad. Por cada metro cuadrado nos llega una potencia máxima de 1 kW/m2, lo que signifca que, a lo largo de un día soleado de julio, puede llegarnos en una superficie horizontal una energía de, por ejemplo, 6 kWh/m2. Esta magnitud se denomina irradiación solar. En segundo lugar, de esta irradiación solar, una placa fotovoltaica aprovecha algo menos del 20%. El resto de la energía no se aprovecha, bien porque la radiación se refleja o porque se transforma en calor que debe disipar el equipo.
En tercer lugar, la energía eléctrica producida llega al ventilador y este la transforma en movimiento mecánico que, a su vez, impulsa el aire. Es decir, transformamos la electricidad en movimiento mecánico. No obstante, no toda ella se transforma, una parte se convierte en calor que hay que disipar. Por ejemplo, un ventilador pequeño puede transformar en movimiento útil del aire no más del 50%. El resto se pierde, nuevamente, en calor.
En resumen, hay dos transformaciones básicas, una de radiación solar a electricidad y otra de electricidad a energía mecánica. Junto con estas dos transformaciones deseadas hay otra indeseada, las pérdidas del sistema en forma de calor (no hay que olvidar que es la forma más degradada de energía). Si hacemos operaciones con los datos ejemplificados, tenemos que se aprovecha el 10% de la radiación solar en un propósito útil: mover el aire.
.jpg)






























































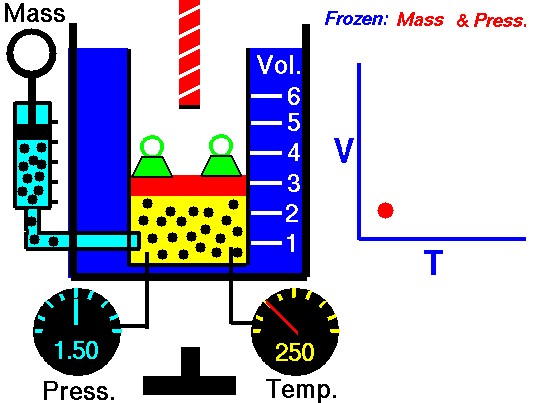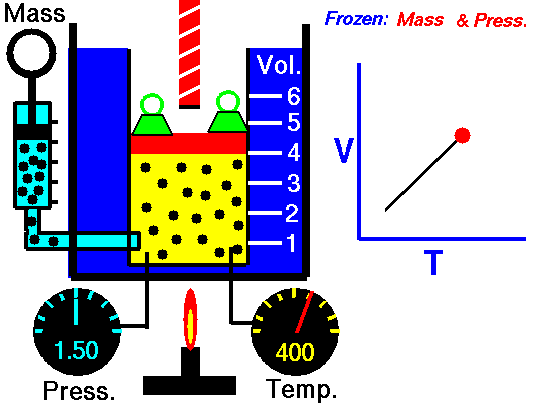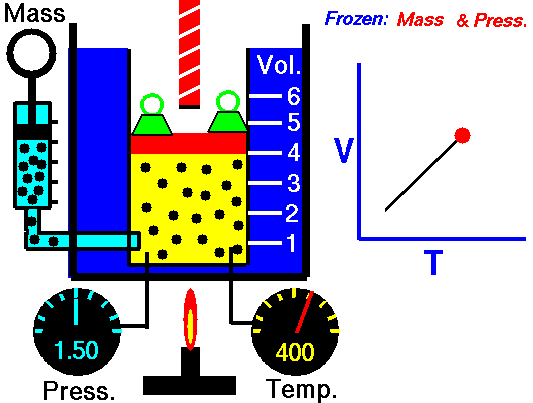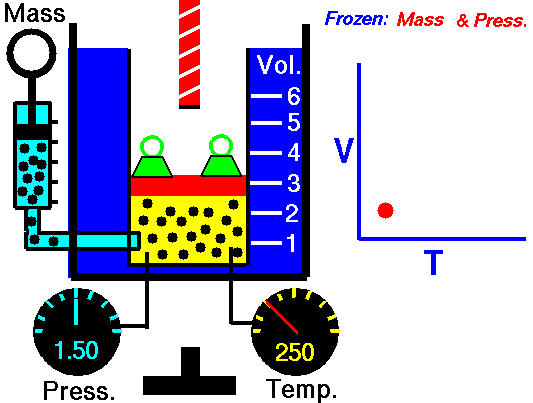


 Este valor constante que aparece en la anteruor fórmula, se demuestra que equivale al producto de una constante R por la masa del gas en moles. Con lo que la ecuación de los gases perfectos se puede expresar, de forma general, del siguiente modo:
Este valor constante que aparece en la anteruor fórmula, se demuestra que equivale al producto de una constante R por la masa del gas en moles. Con lo que la ecuación de los gases perfectos se puede expresar, de forma general, del siguiente modo:














 Observa que la Q, normalmente es energía térmica y, con el punto encima, indica una potencia térmica. Las potencias que no son térmicas, frecuentemente utilizan P.
Observa que la Q, normalmente es energía térmica y, con el punto encima, indica una potencia térmica. Las potencias que no son térmicas, frecuentemente utilizan P.