Cálculos financieros a interés simple.
Caso práctico

 Jorge y Pilar, conscientes de que para realizar con responsabilidad y eficacia su trabajo, precisan de una sólida formación, se han propuesto recopilar en un cuaderno las expresiones matemáticas, fórmulas y tipos de cálculos que se les pueden plantear cuando deban comprobar los estados bancarios y, llegado el caso, cuando deban negociar nuevos productos con las entidades financieras. Conocimientos que también les serán de ayuda para su vida personal.
Jorge y Pilar, conscientes de que para realizar con responsabilidad y eficacia su trabajo, precisan de una sólida formación, se han propuesto recopilar en un cuaderno las expresiones matemáticas, fórmulas y tipos de cálculos que se les pueden plantear cuando deban comprobar los estados bancarios y, llegado el caso, cuando deban negociar nuevos productos con las entidades financieras. Conocimientos que también les serán de ayuda para su vida personal.
A modo de ejemplo, se han preguntado qué necesitan saber para determinar los intereses y la rentabilidad obtenida por depositar su dinero en una entidad durante diferentes periodos de tiempo y a diferentes tipos de interés.
Este sencillo supuesto se plantea en un nivel personal. Pero en su breve experiencia laboral se han dado cuenta que las relaciones entre empresas y entidades financieras son mucho más variadas; y los casos que se dan son mucho más complejos.
Metidos en faena, su primera tarea va a ser recordar y recopilar los fundamentos matemáticos en los que se basan los cálculos financieros.

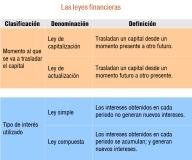
1.- El interés y las leyes financieras.
Cuando en el contexto de una conversación sobre el dinero, se menciona la palabra interés, ¿qué te sugiere?: la cantidad que puedes recibir por dejarlo depositado en un banco; o, con mayor frecuencia, la que deberás pagar por el préstamo que has pedido.
Evidentemente no es lo mismo ceder nuestro dinero a una entidad y percibir una remuneración, que pedir prestada una cantidad de dinero; en cuyo caso, además de devolver la cantidad recibida, deberemos pagar unos intereses. Que siempre son más altos que cuando cedemos nuestro dinero.
Recuerda que un préstamo es un acuerdo por el cual una persona, llamada prestamista, deja una cosa (normalmente dinero) a otra, llamada prestataria, con la condición de que éste se la devuelva. El prestamista percibirá el capital entregado, más una recompensa, que es el interés.
Las razones por las que el prestamista percibe un interés, son:
- Para resarcirse de la pérdida de valor del dinero como consecuencia del paso del tiempo (inflación).
- Como compensación por su renuncia a la disponibilidad del capital durante el tiempo que lo ha prestado.
- Para recompensar el posible riesgo que asume de no recuperar la cantidad prestada.
Igualmente, depositar una cantidad ahorrada supone renunciar, durante un periodo de tiempo, a disponer de esa cantidad de dinero. Esta “no disponibilidad” se ve recompensada con una contraprestación monetaria que es el interés.

Pero tanto el importe del interés a pagar por un préstamo o a recibir por el depósito de los ahorros, dependerá de tres variables:
- De la cantidad ahorrada o prestada –capital inicial-; expresada en euros.
- Del tiempo que ha durado la operación; que se suele indicar en años, meses o días.
- Del tipo o tasa de interés al que se ha realizado la misma, que aunque se expresa en tanto por ciento, en los ejercicios trabajaremos con tantos por uno.
Reflexiona
El interés que pagan las entidades financieras por el dinero que tenemos en cuentas de depósito o en imposiciones, es muy inferior al que nos cobran cuando nos conceden un préstamo.
Evidentemente, debe ser así para cubrir los gastos que el desarrollo de una actividad económica lleva consigo.
Pero, ¿te parece razonable la diferencia que hay entre los intereses que cobran por el dinero que nos prestan, y el que recibimos por nuestros depósitos?
Por otra parte, ¿qué opinas de las comisiones que cobran por los servicios que prestan?
1.1.- Las leyes financieras.
Con lo visto te preguntarás ¿qué puedo hacer con estas tres variables, para calcular el coste o el rendimiento de un préstamo o de un depósito? Porque tu experiencia te dice que esto del interés no es tan sencillo como coger tres datos, mezclarlos y ya está. Es más complejo.
Sí; es más complejo. Pero no tanto. Aunque es importante ir poco a poco y asegurando los conceptos.
Empecemos por los conceptos teóricos: una ley financiera es una herramienta matemática que relaciona las tres variables mencionadas y que nos va a permitir conocer, por ejemplo, el importe total a pagar por un préstamo. Por lo tanto, una ley financiera relaciona la cantidad (capital), el tiempo y el tipo de interés con el que se ha realizado una operación de carácter financiero.
Una ley financiera nos permite trasladar un capital desde un momento a otro distinto. Es por tanto una función que depende del capital, del tiempo y del tipo de interés.
Autoevaluación
Autoevaluación
2.- Ley financiera de capitalización simple.
Caso práctico


Una vez establecido el marco teórico, Jorge le propone a Pilar que inicien el repaso por lo más evidente y sencillo: la capitalización simple.
Pilar se muestra absolutamente de acuerdo. Pues recuerda que, en su etapa de estudiante, cuando logró comprender el significado y las relaciones que se dan entre los elementos de la capitalización simple, adquirió una enorme seguridad para aprender el resto de cálculos financieros.
Jorge, pensando ahora en el día a día, añade a esta reflexión que cuando queramos calcular el interés, en cualquier situación de nuestra vida, necesitaremos estos elementos.
2.1.- Introducción a la ley financiera de capitalización simple.
Si al pasar por delante de una oficina bancaria ves un cartel que indica: Depósito al 5%. Mínimo 3.000 euros.
¿Sabrías qué tipo de operación financiera está aplicando el banco? Y ¿qué rendimiento vas a obtener si haces este depósito? Con este apartado pretendemos dar respuesta a estas y a otras dudas.
Te recordamos que según lo explicado en el aparado anterior, una ley de capitalización simple es aquella que traslada un capital desde un momento presente a otro futuro (capitalización); y los rendimientos obtenidos en cada periodo de tiempo, no generan nuevos rendimientos (simple).
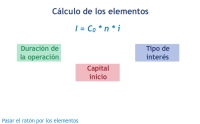
Los elementos que vamos a necesitar para operar con esta ley de capitalización simple, son:
- C0: capital inicial. Cantidad que el ahorrador ha depositado o que el prestamista ha entregado al prestatario al inicio de la operación.
- i: tasa o tipo de interés, expresado en tanto por uno. Tipo al que se ha prestado o depositado el capital inicial.
- n: duración de la operación, expresado en años, meses, días,... Este elemento debe estar expresado siempre en la misma unidad de tiempo que el tipo de interés. Es decir, con tipo de interés anual, el tiempo en años; con un tipo de interés mensual, el tiempo en meses.
- I: rendimiento o interés generado por el depósito o producido por el préstamo.
- Cn: capital final o montante. Que será igual al capital inicial más el interés generado.
En la imagen puedes apreciar estos elementos para una operación de un único periodo.

Autoevaluación
2.2.- Demostración matemática.
Bueno, ya te hemos presentado los elementos que vamos a utilizar, ¿cuál debe ser el siguiente paso? Evidentemente ver qué relación hay entre ellos. Y para ello necesitamos algo de matemáticas.
Importante: en capitalización simple, el interés ─I─ de cada periodo, es: 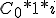
Con este bagaje, vamos a proceder a demostrar cómo podemos calcular el capital final ─Cn─, para un determinado periodo de tiempo ─n─, y a un tanto por uno ─i─ anual.
Al finalizar el primer año, el capital final será el inicial más los intereses de 1 año: 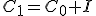
Sustituyendo el Interés por su valor: 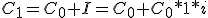
Y sacando factor común C0: 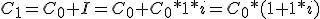
Al finalizar el segundo año, el capital final será el inicial en este segundo año ─C1─, más los intereses producidos en el 2º año (que son iguales a los del 1º): 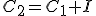
Sustituyendo el capital inicial y el Interés por su valor: 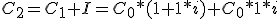
Y sacando factor común C0: 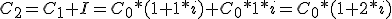
Al finalizar el tercer año, el capital final será el inicial de este tercer año más los intereses producidos en el 3er año (iguales a los del 1º y a los del 2º): 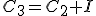
Sustituyendo el capital inicial y el Interés por su valor: 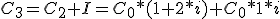
Y sacando factor común C0: 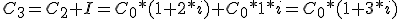 y así en los sucesivos años.
y así en los sucesivos años.
Por lo tanto, al finalizar el año ─n─, el capital acumulado final será: 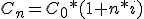

Para aplicar correctamente esta fórmula debemos dar 2 precisiones:
- El valor de este elemento ─i─ a utilizar será en tanto por uno; esto quiere decir que si nos lo dan en tanto por ciento, antes de aplicar la fórmula deberemos dividirlo por 100, para pasarlo a tanto por uno.
- El tanto por uno ─i─ se va a referir, mientras no se diga lo contrario, a tanto por uno anual.
Con la fórmula: 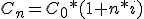 formula podemos calcular el capital final ─Cn─ que pagaremos u obtendremos, aplicando la ley financiera de capitalización simple, de un capital ─C0 (capital inicial)─, al final de un periodo ─n─, si se le aplica un tipo de interés ─i─.
formula podemos calcular el capital final ─Cn─ que pagaremos u obtendremos, aplicando la ley financiera de capitalización simple, de un capital ─C0 (capital inicial)─, al final de un periodo ─n─, si se le aplica un tipo de interés ─i─.
De tal manera que una vez determinado el capital final, calcular el interés obtenido, es muy sencillo, basta con restarle el capital inicial:
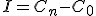
2.3.- Cálculo de los elementos del interés simple.
En el apartado anterior hemos visto que el Interés se puede obtener como diferencia entre el capital final -Cn- y el capital inicial -C0-. Pero tú, seguramente, lo que quieres es determinar el rendimiento que puedes obtener de tus ahorros directamente, sin necesidad de calcular previamente el capital final.
En este apartado vamos a demostrar matemáticamente cómo se obtiene el Interés y el resto de elementos de la capitalización simple, a partir de dos expresiones que ya conocemos:
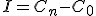
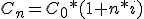
A partir de la expresión del Interés: 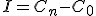
Sustituyendo el capital final: 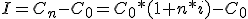
Quitando paréntesis y sacando factor común C0:
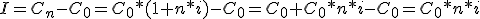
Tras lo cual hemos obtenido la fórmula que calcula el interés a partir del capital inicial:
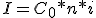
¿Qué hemos obtenido?: Que el interés es proporcional al capital, al tiempo y al tanto de interés aplicado. Por lo tanto, a mayor capital, más interés; cuanto mayor sea el tiempo, mayor será también el interés; y lógicamente, a mayor tipo de interés, mayor rendimiento o interés.
De esta expresión del Interés, podemos deducir el valor del resto de elementos:
Autoevaluación
Solución
2.4.- Cómo resolver ejercicios de interés simple.
Para analizar cómo resolver un supuesto de capitalización simple y practicar con la aplicación de las fórmulas vistas en el apartado anterior, te proponemos el siguiente supuesto:
Pilar tiene unos ahorros que de momento no necesita hacer uso de ellos. La Caja de Ahorros donde tiene domiciliada la nómina ha lanzado una campaña que ofrece un 5% de interés si se depositan al menos 3.000 euros, a un plazo fijo durante tres años. Decide hacer cuentas para conocer qué interés puede obtener; y en consecuencia qué capital tendrá tras los 3 años.
En primer lugar debemos identificar todos los datos que el supuesto nos da. Éstos son:
- Capital inicial: C0 = 3.000 euros
- Tasa o tipo de interés: 5 % anual. Que pasado a tanto por uno: i = 0,05 anual.
- Número de periodos: n = 3 años. Recuerda que el número de periodos debe expresarse en la misma unidad de tiempo que el tipo de interés.
Una vez “presentados” los elementos que el supuesto propone; debemos plantearnos qué nos pide y cómo calcularlo. El enunciado plantea que obtengamos el interés, ¿recuerdas la expresión matemática que permite su cálculo?
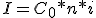
Sustituyendo los valores, obtendrás el siguiente resultado: 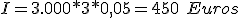
Por lo tanto el capital final será:
Y ahora, ¿cómo haríamos para calcular cualquier elemento? Veamos qué fórmulas utilizar:
Cálculo del capital que ha depositado:
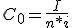
sustituyendo los valores
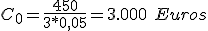
Para calcular el número de periodos:
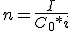
sustituyendo los valores
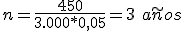
Y el tipo de interés:
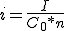
sustituyendo los valores
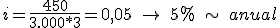
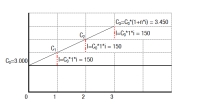
En la imagen puedes apreciar dónde se sitúa, en una proyección temporal, cada elemento con su correspondiente valor.
2.5.- El interés para periodos no anuales.
Te habrás dado cuenta que en los ejercicios que hemos realizado hasta el momento sólo nos hemos referido a tantos anuales de interés y el tiempo lo hemos expresado en años. Y te habrás preguntado ¿qué pasa si alguno de los dos elementos, o los dos, están expresados en unidades diferentes al año? Algún tipo de conversión deberemos realizar, ¿no? Vamos a verlo.
Nunca debes olvidar que el número de periodos ─n─ y el tipo de interés ─>i─ tienen que expresarse en la misma unidad de tiempo. De tal manera, que cuando no estén referidos a la misma unidad de tiempo, será preciso transformar uno de los dos; o los dos.
Por costumbre o conveniencia comercial, el tipo de interés suele ser anual. De tal manera que si no se indica otro periodo de tiempo, se considerará que es anual. Por ello, lo más habitual será, a partir de un tanto de interés anual, transformar el número de periodos para expresarlo en periodos anuales (aunque obtengamos una fracción o decimales).
 Este tipo de transformaciones son sencillas, ya que basta con dividir el tiempo dado, por el número de periodos que la unidad de tiempo está contenida en un año. Así, por ejemplo:
Este tipo de transformaciones son sencillas, ya que basta con dividir el tiempo dado, por el número de periodos que la unidad de tiempo está contenida en un año. Así, por ejemplo:
3 semestres, son 3/2 = 1,5 años
9 trimestres, son 9/4 = 2,25 años
30 meses, son 30/12 = 2,5 años
540 días, son 540/360 = 1,5 años.
Como has podido comprobar, hemos dividido el número de periodos por las veces que éste está contenido en un año. Con la salvedad que cuando se trata de días, consideramos que el año tiene 360 días (se trata, nuevamente, de una conveniencia comercial que más adelante comentaremos).
Ejercicio resuelto
¿A cuánto ascendería el interés de los 3.000 euros depositados en una entidad financiera al 4% anual, si en lugar de 1 año, el plazo de la imposición es de 9 meses? ¿y si el plazo fuera de 300 días?
Para calcular la incógnita del ejercicio, seguiremos el siguiente proceso:
- determinar los elementos que da el enunciado
- establecer la fórmula a utilizar
- sustituir valores y calcular el resultado
2.6.- Tantos Equivalentes.
Ya has visto cómo transformar los periodos de tiempo. Seguro que ahora quieres analizar cómo transformar el tipo de interés sin que se vea modificado el resultado. ¿Se te ocurre qué criterio aplicaremos?
Vayamos primero con una afirmación categórica: Dos tantos o tipos de interés, son equivalentes, cuando aplicados a un mismo capital inicial, durante un mismo periodo de tiempo, producen el mismo Interés o generan el mismo capital final.
En capitalización simple, si el tanto por uno anual ─i─ lo queremos transformar en tanto por uno de interés referido a una fracción de año, procederemos a dividirlo por el número de veces ─k─ en que fraccionamos el año.

La expresión matemática será: 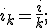 de donde, despejando:
de donde, despejando: 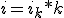
i es el tanto por uno anual
k es el número de veces que una unidad de tiempo está contenida en un año (semestres, 2; trimestres, 4; meses, 12; días, 360)
ik el tanto por uno referido a una fracción k del año
Por lo tanto, en capitalización simple, los tantos de interés son proporcionales a los periodos de tiempo.
| i2 = tanto por uno semestral | 1 año = 2 semestres |
| i4 = tanto por uno trimestral | 1 año = 4 trimestres |
| i12 = tanto por uno mensual | 1 año = 12 meses |
Dos tantos unitarios ─i─ (anual) e ─ik─ (k-esimal) son equivalentes, cuando aplicados al mismo capital ─C0─, durante el mismo tiempo ─n─, producen el mismo interés ─I─.
Autoevaluación
2.7.- Año comercial y año natural o civil.
Como habrás podido observar en las actividades que el tiempo estaba expresado en días, para calcular su equivalente en años, hemos considerado que el año tiene 360 días. A esta práctica se la denomina aplicar “año comercial”. ¿Te parece correcta? ¿O tal vez deberíamos tomar el año por los días naturales que tiene?
Se utiliza el “año comercial” (360 días), simplemente porque resulta más fácil de utilizar matemáticamente, por ser divisible por 2, 3, 4, 6, 12, etc.
Pero en la práctica bancaria se utiliza también el “año civil”; también denominado “año natural”. Que consiste en asignar a un año 365 días (o 366 días si es año bisiesto). Evidentemente el “año civil” se aplicable sólo cuando el tiempo se expresa en días, no para meses o trimestres, por ejemplo.
La forma de calcular el interés es exactamente igual en un caso como en otro; salvo por el cociente a aplicar para pasar los días a años.
Los ejemplos y supuestos planteados en este módulo, salvo que se indique lo contrario, se resolverán aplicando año comercial (360 días).
Para comprender la diferencia entre calcular el interés aplicando “año comercial”, denominado interés comercial; o “año civil”, conocido como interés natural o civil, vamos a analizar el siguiente ejercicio resuelto.
Ejercicio resuelto
Vamos a suponer que como consecuencia de la acumulación de varios pagos a final de mes, se han generado en nuestra cuenta corriente “números rojos”, es decir que el banco ha tenido que realizar unos pagos por nuestra cuenta, porque no había saldo suficiente, por un importe de 500 euros.
El banco cobra en las operaciones de descubierto bancario un 9% de interés anual. Y el número de días que hemos tenido saldo deudor ha sido de 9. Queremos saber cuánto nos cargará el banco en concepto de intereses, por esta situación de descubierto, aplicando el criterio de “año comercial” y el de “año civil”.
Pasos a seguir para resolver el supuesto:
- Primero vamos a ver qué elementos nos proporciona el enunciado:
- A continuación indicaremos qué fórmula vamos a emplear para calcular el Interés.
- Y por último, sustituiremos los valores en la expresión anterior.
3.- Ley financiera de actualización simple.
Caso práctico


Jorge le manifiesta a Pilar su satisfacción por la recopilación que hasta el momento ha realizado. Pilar le hace ver que no han hecho más que iniciar el trabajo que se han propuesto.
Pilar le plantea un nuevo caso parecido a lo analizado:
-¿Qué elementos y expresiones matemáticas deberemos utilizar, si lo que queremos es calcular el valor que tiene hoy una deuda que vence, por ejemplo dentro de 3 meses?
Jorge, sin pensar más, le contesta: eso es como el interés pero hacia atrás.
-Más o menos, le responde Pilar; tras lo cual le dice:
-En las operaciones comerciales y sobretodo, en las financieras a corto plazo que realizamos con las entidades financieras, es muy importante la ley de actualización simple.
3.1.- El Descuento.
En el apartado anterior has visto cómo calcular el valor que tu dinero puede tener dentro de un tiempo, calculando el interés que ha generado después de varios periodos. Pero, ¿cómo calcularías la cantidad a pagar hoy por una deuda que tiene su vencimiento en un futuro?
En definitiva, vamos a estudiar el valor que tendrá el capital ─Cn─, en el momento actual ─C0─.
Al pagar una cantidad anticipadamente, es decir antes de su vencimiento, lo que se hace es sustituir un capital aplazado, con vencimiento en el futuro, por otro actual. A la diferencia existente entre ambos se le denomina descuento.
Por lo tanto el capital inicial se obtendrá de restar, del importe del capital final de cada periodo, el descuento generado en ese mismo periodo, que denominaremos ─D─.
Descuento es la cantidad que se deduce a un capital al adelantar su fecha de vencimiento.

Hasta el momento hemos denominado a ─i─: tipo o tasa de interés.
En las operaciones de actualización o descuento, también se suele denominar tipo o tasa de descuento; incluso se puede expresar como ─d─ en lugar de ─i─. Nosotros vamos a utilizar la misma expresión: ─i─; aunque en alguna ocasión lo denominemos como tasa o tipo de descuento.
Autoevaluación
3.2.- Capital inicial.
Antes de proseguir. Asegúrate que has comprendido el significado del descuento. Porque lo que vas a estudiar en los siguientes apartados es similar al interés, pero no es lo mismo. Aunque creas que estás volviendo a estudiar algo que ya conoces; procura hacerlo como si fuera todo nuevo.
En este apartado vamos a demostrar cómo calcular el valor inicial ─C0─, que tendrá un capital final ─Cn─, en el momento “0” (periodo “0”).
Para facilitar la comprensión de este desarrollo matemático, vamos a limitar el análisis a tres periodos. De tal manera, que una vez demostrado cómo se obtiene el capital inicial para los tres periodos, la fórmula será válida para cualquier número ─n─ de periodos.
Seguimos utilizando leyes financieras simples. Por lo que el descuento de cada periodo será:
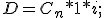 para nuestro caso:
para nuestro caso: 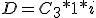
Al inicio del periodo “3” el capital inicial será: 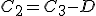
Recuerda:
- C3: Capital final del periodo tres.
- C2: Capital final del periodo dos; y por lo tanto, capital inicial del periodo tres.
Sustituyendo el descuento: 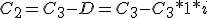
Y sacando factor común C3: 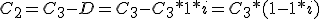
Al inicio del periodo “2”, el capital inicial será: 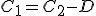
Sustituyendo C2 y el descuento: 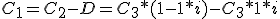
Y sacando factor común C3: 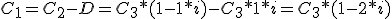
Al inicio del periodo “1” el capital inicial será: 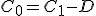

Sustituyendo C1 y el descuento: 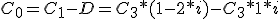
Sacando factor común C3: 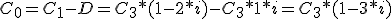
De tal manera que la fórmula general será: 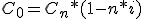
Al igual que ocurría con las leyes de capitalización simple, la ley de actualización simple no tiene en cuenta el descuento generado en los períodos anteriores, sino que determina el capital inicial ─Co─, calculando el descuento únicamente sobre el capital final ─Cn─.
Cuando se opera con leyes de actualización simple, se suele utilizar una terminología diferente a la empleada hasta ahora. Así:
Al capital final ─Cn─ se le denomina Nominal (N)
Al capital inicial ─C0─ se le denomina Efectivo (E)
De tal forma que si en el interés: I = Cn - C0; en el descuento: D = N - E
No obstante, por mantener una terminología uniforme a lo largo de todo el módulo, aunque nos refiramos a Nominal y Efectivo, en los cálculos utilizaremos ─Cn─ y ─C0─.
3.3.- Cálculo del descuento comercial y del resto de elementos.
Llegado a este punto, te dirás que muy bien las demostraciones y los análisis matemáticos. Pero cómo se aplican en la vida comercial. Tienes razón. En la práctica, el concepto fundamental es el de descuento comercial. Pero vas a ver, que después de lo estudiado resulta muy sencillo calcular su valor.
Esta denominación de descuento "comercial", es consecuencia de su utilización habitual en la práctica mercantil y bancaria. Su cálculo se realiza a partir del capital final; e independientemente del número de días que se considere cada año.
Nosotros conocemos hasta ahora dos expresiones: 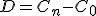 y
y 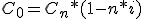
Sustituyendo:
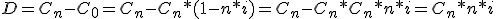
En definitiva: 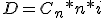
Como te demostramos en la presentación adjunta, de la expresión del descuento comercial podemos, despejando, calcular el capital final, el tiempo y la tipo de interés si conocemos los demás elementos. Recuerda que el tiempo siempre debe estar expresado en la misma unidad que la tasa o tipo de interés.
Ejercicio resuelto
Una letra de 300 euros, descontada al 6% anual, ha originado un capital inicial o Efectivo de 292 euros ¿cuántos días se ha descontado?
Recuerda que, para resolver un supuesto, seguimos tres pasos:
- determinar los elementos que da el enunciado
- establecer la fórmula a utilizar
- sustituir valores y calcular el resultado
Autoevaluación
3.4.- Métodos abreviados para el cálculo del interés y del descuento.

En determinadas operaciones financieras, como más adelante veremos, es preciso calcular el interés o el descuento de forma reiterada; por lo que se utilizan métodos abreviados para agilizar y simplificar los cálculos. Hay varios métodos abreviados, pero te vamos a presentar únicamente uno, el de números comerciales. Que en unidades posteriores volveremos a utilizar.
El método abreviado de Números Comerciales –NC-, consiste en determinar la suma de los productos de cada Nominal o capital final, por los días que se descuenta.
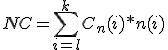
Donde ─k─ es cada uno de los capitales, con su respectivo vencimiento.
Este método es útil cuando se aplica a varios capitales con sus vencimientos respectivos y la misma tasa de interés o descuento. Para su aplicación, primero se calculan los números comerciales de todos los capitales, y a continuación se aplica la fórmula del descuento comercial.
Si queremos calcular el descuento de una remesa de efectos con “k” capitales diferentes, el cálculo del descuento será:
El método abreviado de Números comerciales –NC-, consiste en determinar la suma de los productos de cada Nominal o capital final, por los días que se descuenta:
De tal manera que aplicado sobre una remesa de efectos con diferentes nominales, el cálculo del descuento será:
Ejercicio resuelto
Calcular el efectivo o capital inicial obtenido al descontar 3 letras de 500, 600 y 700 euros, a una tasa del 8% durante 60, 70 y 80 días respectivamente, con el método abreviado de números comerciales.
Recuerda el proceso que seguimos para resolver los ejercicios.
Autoevaluación
Solución
4.- La equivalencia financiera.
Caso práctico


Jorge y Pilar ya se están elaborando unos buenos apuntes para determinar el interés y el descuento. Pero saben que esto no es más que el soporte teórico de todo lo que quieren lograr.
Pilar le cuestiona a Jorge que si un cliente de la empresa quisiera cancelar varias de sus deudas mediante la realización de un pago único, ¿qué conocimientos de los adquiridos debería aplicar?
Jorge ha actualizado sus conocimientos con el trabajo de recopilación que están llevando a cabo; y no duda al responder:
-Aplicaría la ley de actualización simple.
Pilar le ha formulado esta reflexión, no para poner a prueba a Jorge, sino para resaltar que este tipo de operaciones o supuestos son habituales; y no sólo para cancelar deudas.
Por ello le propone que continúen, su tarea de recopilación, con el análisis de la equivalencia financiera.
4.1.- Equivalencia financiera de capitales.

Vamos a suponer que quieres comprarte un coche determinado y has pedido precio a dos concesionarios: uno te pide 18.000 euros al contado; y otro, 20.000 euros a dos años. ¿Qué opción elegirías?
Independientemente de tu situación financiera, es decir, de tu disponibilidad para hacer frente a estos pagos, te interesará conocer cual de las dos, desde un punto de vista financiero, te interesa más.
Analicemos la situación: tenemos dos capitales de diferente cuantía y con vencimientos diferentes; y nos preguntamos cuál de ellos es la mejor opción financiera; es decir, con cuál de las dos desembolsaré una menor cantidad de dinero o me resultará más barato el coche.
Por lo tanto me estoy planteando que debo comparar ambas opciones. Para ello, no basta con fijarse en sus importes; deberé considerar además la fecha de vencimiento. Y, para que la comparación sea homogénea, deberé llevar los dos capitales a un mismo momento o fecha.
Dos o más capitales con importes y fecha de vencimiento diferentes, son equivalentes, cuando trasladados con una determinada ley financiera a una fecha concreta, tienen el mismo valor.
En la práctica se plantean dos tipos de situaciones a partir de varios capitales que se desean sustituir:
- Se conoce el vencimiento del pago único y se quiere calcular el capital equivalente, a los capitales a sustituir
- Se conoce el capital del pago único y se desea calcular su vencimiento. A esta operación se la conoce como de vencimiento común.
Autoevaluación
Rellena los huecos de la siguiente afirmación con los conceptos adecuados:
4.2.- Desarrollo matemático de la equivalencia financiera (I).

Sigamos con el ejemplo de la compra del coche. El precio de venta es de 20.000 euros, a pagar dentro de 2 años; o de 18.000 euros, si se paga en este momento.
Suponiendo que el concesionario que te ha dado el precio a dos años, te ofrece pagar al contado con un 5% de descuento; tu duda sería determinar cuál de las dos opciones te interesa más, desde un punto de vista financiero:
Para decidir sobre una u otra opción, evidentemente debes comparar ambas opciones en un determinado momento.
Para lo cual aplicamos el principio de equivalencia financiera. El cual implica que se debe cumplir la siguiente igualdad: valor de un capital (pago) en un determinado momento, igual al valor actual del capital o capitales sustituidos (deudas), en ese mismo momento. Si tomamos el origen, sería:
C0 (deudas) = C0 (pago)
Donde: 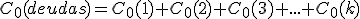
Siendo ─k─ el número de deudas. La fecha en la que se realiza la sustitución de unos capitales por otros, se le denomina época. Que cuando no se indica una fecha concreta, se toma el primer vencimiento.
Para facilitar la resolución de este tipo de ejercicios vamos a utilizar el método de Números Comerciales, porque, como ya sabemos, permite simplificar el cálculo de los intereses cuando los capitales son varios.
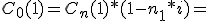
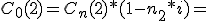
...

![]()
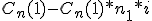
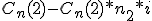
...
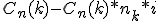
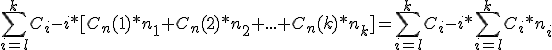
En definitiva: 
4.2.1.- Desarrollo matemático de la equivalencia financiera (II).

Con la explicación del apartado anterior, hemos obtenido el capital inicial de las deudas en el momento fijado como época. Que, para que se cumpla el principio de equivalencia financiera, es también el capital inicial, en este momento, del pago único:
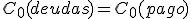
En este mismo momento (época), el capital inicial del pago se obtendrá mediante la expresión:
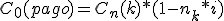
Siendo ─n─, el número de periodos que hay desde la época hasta el vencimiento del pago único y ─k─ el número de pagos.
Si de esta expresión despejamos el capital final, obtendremos:
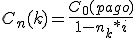
En definitiva, con esta fórmula, determinamos el capital final que sustituye a varios capitales con sus correspondientes plazos de vencimiento por un único capital en el vencimiento que corresponda, de forma que este capital sea equivalente a todos los demás.
Ejercicio resuelto
Retomemos el ejemplo del coche del apartado anterior. Qué datos planteábamos:
Un concesionario: 20.000 euros, a 2 años; y un 5% de descuento, si se paga al contado.
El otro concesionario: 18.000 euros, al contado.
Para decidir qué opción nos interesa, vamos calcular el valor de ambas opciones en un momento concreto: a día de hoy.
Capital actual de los 20.000 euros, con vencimiento a 2 años y tipo de descuento del 5%:
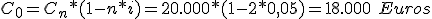
Es decir, ambas ofertas son financieramente equivalentes en el origen.
Autoevaluación
Solución
4.3.- Cómo calcular el capital que sustituye a otros.

Las demostraciones matemáticas están bien y son necesarias. Pero no son suficientes ¿verdad? Por ello, vamos a plantear dos supuestos con el fin de explicarte de una forma práctica, cómo resolver los dos casos de equivalencia financiera que te hemos planteado.
Vamos con el primer supuesto: Se desean sustituir tres efectos de nominales 1.000, 2.000 y 3.000 euros con vencimiento a 20, 40 y 60 días por un único pago, cuyo vencimiento sea a 90 días. Si se aplica una tasa de interés del 5% ¿cuál será el importe de este pago? Como el tiempo viene expresado en días, la base a utilizar en la fórmula del cálculo de los intereses será 360.
Primero calculamos el valor actual o efectivo de los capitales a sustituir:
| Capitales | Vencimiento | Números Comerciales |
|---|---|---|
| 1.000 | 20 | 20.000 |
| 2.000 | 40 | 80.000 |
| 3.000 | 60 | 180.000 |
| 6.000 | 280.000 |
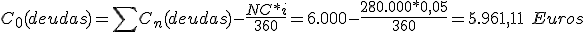
Por lo tanto ya sabemos que estos tres pagos van a ser sustituidos por un único capital cuyo valor efectivo en el origen es de 5.961,11 euros, que vence dentro de 90 días. Nos falta calcular su importe.
Cn (pago) = ¿?
C0 (pago) = 5.961,11 euros
n = 90 días
La fórmula a aplicar será: 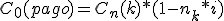
despejando: 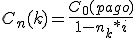 y sustituyendo:
y sustituyendo: 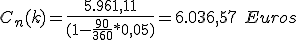
Autoevaluación
4.4.- Cómo calcular el vencimiento del capital que sustituye a otros.

En este apartado te vamos a plantear la segunda situación que te anticipábamos: ¿Cómo calcular la fecha en la que se pueden cancelar conjuntamente dos o más deudas, que vencen en fechas diferentes, con la entrega de una cantidad distinta?
Se desean sustituir tres efectos de nominales 100, 200 y 300 euros con vencimiento a 30, 60 y 90 días por un único pago de 597 euros. Si se aplica una tasa de interés del 4% ¿cuál será el vencimiento del nuevo efecto? Como el tiempo viene expresado en días, la base a utilizar en la fórmula del cálculo de los intereses será 360.
Primero calculamos el capital inicial o efectivo de los capitales a sustituir:
| Capitales | Vencimiento | Números Comerciales |
|---|---|---|
| 100 | 30 | 3.000 |
| 200 | 60 | 12.000 |
| 300 | 90 | 27.000 |
| 600 | 42.000 |

Por lo tanto ya sabemos que estos tres pagos van a ser sustituidos por un único capital de 597 euros, cuyo valor efectivo en el origen es de 595,33 euros. Nos falta calcular su vencimiento.
Cn (pago) = 597 euros
C0 (pago) = 595,33 euros
Descuento del pago = Cn – C0 = 1,67 euros
Luego el vencimiento será:
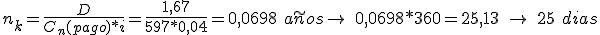
Autoevaluación
5.- Comisiones bancarias.
Caso práctico


Pilar le hacer ver a Jorge que la mayoría de las operaciones a las que le son aplicables los cálculos estudiados, se realizan a través de las entidades financieras.
Y éstas, como empresas de servicios y no sólo financieras, cobran unas cantidades por su labor de intermediación.
Jorge, sin dejarla terminar hablar dice:
-¡las comisiones!
-Exacto, responde Pilar
5.1.- Características de las comisiones.
Seguro que no hace falta que te digamos que son las comisiones. De sobra sé lo que son ¡pensarás!.
Por ello, en este apartado únicamente te vamos a presentar los diferentes tipos de comisiones que suelen cobrar las entidades financieras y a recordar cómo se calculan.
Las comisiones son cantidades que cobran las entidades financieras por los servicios de intermediación o gestión que prestan a sus clientes.
El cobro de comisiones bancarias por las entidades de crédito está sujeto a unas reglas fijadas por el Banco de España. Las más importantes son:
- Las tarifas, o precios, de las comisiones bancarias son libres. Es decir las entidades pueden poner los importes que deseen, excepto en unas pocas operaciones, como la cancelación o amortización anticipada de un préstamo hipotecario.
- Las comisiones bancarias y los gastos deben responder a servicios efectivamente prestados.
- Las comisiones, excepto las correspondientes a servicios de pago, deben aparecer en un folleto redactado de forma clara y fácilmente comprensible.
- En el caso de servicios de pago (transferencias, cuentas, adeudos domiciliados, tarjetas de pago), la entidad deberá informar personalmente y por anticipado del coste del servicio.
- Los importes recogidos en el folleto de comisiones de cada entidad son máximos. No puede cobrarse más de lo recogido.
- Cuando se modifiquen comisiones que afecten a contratos de duración indefinida, deberán comunicarse las modificaciones con una antelación de al menos dos meses.
- Las entidades que trabajen exclusivamente por banca telefónica deberán comunicar por escrito periódicamente a sus clientes la información que es obligatorio incluir en el tablón de anuncios de las oficinas.
- Las entidades que ofrezcan la posibilidad de realizar operaciones a través de Internet deberán incluir también en su propia página Web el folleto de tarifas.
5.2.- Tipos y cálculo de las comisiones.
Ya sabes que los motivos por los que las entidades financieras pueden cobrar comisiones son muy amplios. Por ello no pretendemos enumerar todos, sino que te vamos a presentar, ordenados por tipos de operaciones, algunas de las operaciones que normalmente llevan comisiones.
Ejecuta la siguiente presentación, analiza las que te presentamos y piensa en otras que no incluimos:
Cómo se calculan las comisiones:
El importe a pagar por comisiones se calcula, normalmente, aplicando un tanto por ciento sobre el valor de la operación que la origina. Y en la mayoría de los casos, las entidades fijan una cantidad mínima. De tal manera, que si el resultado de aplicar el porcentaje mencionado es menor que dicha cantidad mínima, se cobra ésta.
La Ley 16/2009 de servicios de pago, ha incorporado al ordenamiento jurídico español la Directiva 2007/64/CE del Parlamento Europeo, sobre servicios de pago en el mercado interior. El objetivo de esta normativa es garantizar que los pagos realizados en el ámbito de la Unión Europea, transferencias, adeudos y operaciones de pago mediante tarjetas, se realicen con la misma facilidad, eficiencia y seguridad que los pagos nacionales, y de esa forma, contribuir al reforzamiento y protección, de los derechos de los usuarios.
Autoevaluación
Solución
Anexo.- Licencias de recursos.
| Recurso (1) | Datos del recurso (1) | Recurso (2) | Datos del recurso (2) |
|---|---|---|---|
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Duboix. Licencia: Libre. Procedencia: http://morguefile.com/archive/display/672252 |
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |