Operaciones bancarias a interés compuesto.
Caso práctico

 Jorge y Pilar comentan, con
satisfacción, el buen trabajo de recopilación que han realizado hasta el
momento; y la seguridad que han adquirido al ver y comprender que esos
conocimientos teóricos, han sabido aplicarlos en operaciones bancarias.
Jorge y Pilar comentan, con
satisfacción, el buen trabajo de recopilación que han realizado hasta el
momento; y la seguridad que han adquirido al ver y comprender que esos
conocimientos teóricos, han sabido aplicarlos en operaciones bancarias.
-¡Todos, no!; corrige Pilar.
Y le comenta a Jorge que todavía le queda por analizar y aplicar los cálculos de capitalización compuesta. Y para ello nada como solicitar y negociar un préstamo.

1.- ¿Qué es un préstamo?

Seguro que no tienes ninguna dificultad para explicar, aunque no sea con los términos precisos, qué es un préstamo. Otra cosa, y con total probabilidad, es que te interesa comprender y saber cómo se determinan las cantidades a pagar en cada periodo para proceder a su devolución.
Por ello, y como definición, te vamos a recordar la que ya vimos en la unidad 2: Un préstamo es una operación financiera consistente en la entrega, por parte de una persona o empresa (denominada prestamista) de una cantidad de dinero a otra (prestatario), con el compromiso de reembolsar una cantidad equivalente, en unos plazos convenidos, junto con los intereses establecidos.
Lo expresado en esta definición, nos permite destacar los siguientes elementos:
- Figuras o personas que
intervienen:
- Prestatario. Es la persona que recibe la cantidad prestada.
- Prestamista. Es la entidad que presta una cantidad al prestatario.
- Cantidades que operan en una
operación de préstamo:
- La cantidad prestada: Se trata de una prestación única.
- Las cantidades
que se pagan para devolverla: Puede ser una contraprestación única (que englobe
el capital prestado más los intereses); pero lo habitual es que sean varias
cantidades formadas por dos partes:
- Devolución de la cantidad prestada. Se denomina amortización.
- Pago de los intereses de esta cantidad.
- Principio financiero aplicado:
- La prestación y las contraprestaciones guardan el principio de equivalencia financiera. Es decir, el importe total prestado es igual a la suma de las contraprestaciones; valoradas a un tipo de interés determinado y en un momento concreto.
En esta unidad vamos a trabajar los elementos de un préstamo, las diferentes formas de calcular las cuotas para su devolución y de forma expresa y detallada, el sistema de amortización progresiva o francés.
Autoevaluación
Rellena los huecos de la siguiente afirmación con los términos adecuados:
1.1.- Factores a considerar en la concesión de préstamos.

Cuando una entidad financiera realiza una operación de activo se arriesga a no recuperar el importe cedido y a no percibir sus correspondientes intereses; o a que no los devuelvan en el plazo establecido.
Por ello, a la hora de conceder un préstamo u otra operación de activo, se tienen en cuenta varios factores:
- Garantía de recuperar la inversión realizada. A las entidades
financieras les interesan operaciones que les ofrezcan suficiente seguridad
para recuperar el importe cedido en los plazos fijados. Y para ello, exigen la
existencia de una garantía definida y evaluable.
Para que a una garantía crediticia se la considere oportuna, ha de cumplir los siguientes requisitos:
- Ser realizable: En el sentido de que debe existir un mercado potencial en el que vender y realizar dichas garantías.
- Poderse valorar: Las garantías han de ser fáciles de valorar en todo momento.
- Poseer estabilidad: Su valor efectivo no debe estar sujeto a importantes fluctuaciones.
- Ser transferible: La transmisión de la misma ha de ser fácil y con bajo coste.
Las garantías pueden ser:
- Personales. Son aquellas que no aseguran la deuda mediante un bien concreto. Se basan en la confianza sobre el cumplimiento de las obligaciones contraídas y en la existencia de un patrimonio suficiente para responder de las operaciones de crédito en cuestión.
- Reales. Son aquéllas en las que se comprometen bienes muebles o inmuebles expresamente determinados al buen fin de la operación. Suelen ser preferidas por los acreedores.
- Cierta correlación entre los plazos fijados para devolver el préstamo y la generación de recursos del bien financiado. Por ejemplo, así como no tiene sentido para realizar un viaje de 15 días, pedir un préstamo a devolver en 5 años; tampoco lo tiene, el pedir financiación para comprar un coche y fijar como plazo de devolución 3 meses. Es decir, se busca correlación entre la finalidad del préstamo con los plazos de devolución.
- Prestar todo tipo de servicios al cliente. Todos somos conscientes que si queremos obtener un préstamo hipotecario de una determinada entidad, ésta nos va a exigir que tengamos domiciliada la nómina en la misma; y por lo tanto, todos los pagos que habitualmente realizamos. Es decir, la entidad financiera, busca obtener otro tipo de rendimientos como consecuencia de la concesión del préstamo.
Autoevaluación
Solución
2.- Sistemas de amortización de préstamos.
Caso práctico

 -Ya sabemos qué es un préstamo y
qué requisitos exigen las entidades financieras para su concesión. Dice Jorge.
-Ya sabemos qué es un préstamo y
qué requisitos exigen las entidades financieras para su concesión. Dice Jorge.
Y añade:
-¿Pero cómo se determinan los intereses a pagar y la cantidad a devolver?
Paula le explica que hay varios métodos. Y aunque sólo uno de ellos se aplica comercialmente; es interesante que analicemos todos.
Y se ponen manos a obra: estudiar los diferentes métodos de amortización y analizar las características de cada uno.
2.1.- Métodos y características de amortización de préstamos.
Un préstamo se solicita porque se necesitan medios líquidos para acometer una inversión o realizar un gasto. Como dijo alguien, el problema de los préstamos es que hay que devolverlos. Y en ello nos vamos a centrar: en los diferentes sistemas o métodos de devolución - también denominado amortización- de los préstamos.
|
Métodos o sistemas |
Características |
|---|---|
|
Reembolso único. |
La contraprestación se realiza al final de la operación. Este pago único incluye los intereses devengados y el capital prestado. |
|
Reembolso único, con pago periódico de intereses. |
Método americano. Supone el pago exclusivo de los intereses en las cuotas de cada periodo, mientras que el capital es amortizado de una sola vez junto con la última cuota. |
|
Amortizable mediante cuotas de amortización fijas. |
Método de cuotas de amortización fijas. La cuantía a pagar en cada periodo es diferente y decreciente; pues aunque es fija la cantidad que se amortiza en cada cuota, los intereses son cada vez menores. |
|
Amortizable mediante cuotas constantes. |
Método francés o de cuotas constantes. La cuantía de las cuotas es siempre la misma a lo largo de la vida del préstamo. |

Los tipos de interés que se fijan en las operaciones financieras, puede ser: fijos, no varían a lo largo de la vida de la operación y permiten conocer con certeza los intereses que se van a pagar en cada periodo, y variables, los cuales dependen de la variación de un valor tomado como referencia (es habitual, fijar el tipo variable de interés en los préstamos hipotecarios, con referencia al Euribor).
Además de pagar los correspondientes intereses, cuando se obtiene un préstamo también se deben satisfacer una serie de comisiones y otros gastos. Las comisiones más frecuentes son:
- Comisión de apertura. La causa que origina este gasto es la simple apertura de la operación.
- Comisión de estudio. Cuando la entidad financiera lleva a cabo un estudio o análisis de la situación de la persona o empresa demandante, cobra este tipo de comisión.
- Comisión de cancelación. Se trata de un porcentaje que se aplica cuando se produce la cancelación total o parcial, antes del plazo fijado, del préstamo.
Autoevaluación
Relaciona los métodos de amortización con las características, escribiendo el número del método en el cuadro correspondiente:
2.2.- Elementos para resolver un préstamo.
Antes de abordar el procedimiento para determinar las cuotas de un préstamo en cada periodo y el cálculo de su evolución hasta su total cancelación, vamos a presentar los elementos que necesitaremos y el formato que utilizaremos para su resolución.
Elementos que intervienen:
- Capital prestado —C0—: Importe prestado por la entidad financiera.
- Tipo de interés al que se presta —i—: Tanto por uno de interés efectivo con referencia a un periodo concreto (mensual; trimestral...).
- Número de periodos de amortización —n—: En la misma unidad que el tipo de interés.
- Cuota a pagar en cada periodo —α—. Este importe dependerá del sistema de amortización que utilicemos.
- Comisiones u otros gastos que la entidad financiera percibe por la operación. Te sorprenderá que el importe de las comisiones no lo utilicemos en los siguientes apartados; pero más adelante te explicaremos porqué las incluimos y para qué necesitamos conocerlas.
La elaboración de un cuadro de amortización de un préstamo no tiene excesiva dificultad si se dispone de una hoja de cálculo instalada en el ordenador. En caso contrario hay que recurrir a una calculadora y los cálculos numéricos pueden resultar pesados y tediosos.
En la imagen siguiente te presentamos las columnas que tendrá el modelo de cuadro que vamos a seguir para la resolución de los préstamos, independientemente de que utilicemos un sistema u otro. Más adelante ya comentaremos ciertas particularidades.
Autoevaluación
Relaciona la forma de representar cada elemento de los préstamos, con su significado, escribiendo el número del elemento en el cuadro correspondiente:
2.3.- Amortización de un préstamo mediante reembolso único.
El estudio de los diversos sistemas de amortización lo vamos a realizar en el mismo orden que te los hemos presentado en el subapartado 2.1.
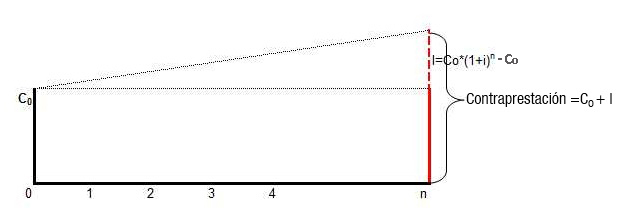
Como ya hemos indicado, una vez recibido el préstamo, la devolución o amortización y el pago de los correspondientes intereses, se realiza mediante un único pago al finalizar el plazo establecido.
Por lo tanto, y como puedes comprobar en la siguiente imagen, en la tabla de amortización del préstamo, únicamente reflejaremos la prestación recibida en la primera línea; y los intereses con el importe a devolver, en la última.
Autoevaluación
2.4.- Amortización de un préstamo mediante reembolso único, con pago periódico de intereses.
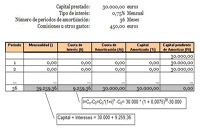
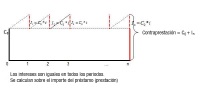
El propio título expresa claramente en que consiste: los intereses se pagan periódicamente; sin embargo, la devolución o amortización del préstamo se realiza mediante un pago único al final de la vida del mismo.
En la tabla siguiente puedes apreciar cómo se realizan los pagos para amortizar un préstamo por este sistema. Los intereses se pagan periódicamente; pero la devolución se lleva a cabo con un pago único y al final de la vida del préstamo.
Autoevaluación
Solución
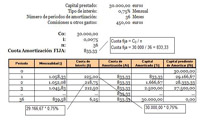
2.5.- Amortización de un préstamo mediante cuotas de amortización fijas.
Tampoco este sistema es habitual. Pero su estudio tiene interés desde un punto de vista educativo. Pues nos permite comparar con otros sistemas y, de esta forma, reforzar la comprensión del que queremos destacar: sistema de amortización mediante cuotas constantes.
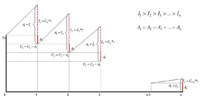
Al igual que en los apartados anteriores, te presentamos una imagen con la representación gráfica del sistema:
Y en la imagen siguiente te mostramos cómo se realiza el cuadro de amortización con este sistema para los datos que hemos utilizado en anteriores casos:
Autoevaluación
3.- Amortización de un préstamo mediante cuotas constantes.
Caso práctico

 Jorge ha comprendido que con lo
recopilado hasta el momento, todavía no ha abordado el método que las entidades
financieras utilizan normalmente.
Jorge ha comprendido que con lo
recopilado hasta el momento, todavía no ha abordado el método que las entidades
financieras utilizan normalmente.
Pilar le anima. Le indica que ya sabe qué elementos y qué esquema se debe seguir para determinar los pagos originados por un préstamo.
Ahora sólo le falta aplicar alguna función matemática concreta para ver el método de cuotas constantes.
3.1.- Elementos de Amortización de un préstamo mediante cuotas constantes.

En primer lugar, vamos a recordar qué elementos intervienen y cómo debemos tratarlos para calcular, primero la cuota; y a continuación el resto del cuadro. Para ello utilizaremos una hoja de cálculo. Es lo más práctico y sencillo. Estos son:
- Capital —C0—: Importe prestado por la entidad financiera. Será una cantidad en euros.
- Tipo de interés —i—: ¡Ojo!; porque nos lo pueden dar como tanto nominal, o como tanto efectivo referido a una unidad de tiempo diferente a la de amortización. Es decir, si no nos dan el tipo de interés referido al periodo en el que se pagan las cuotas (mensual; trimestral...), necesariamente deberemos transformarlo, para expresarlo en tanto por uno de dicho periodo.
- Número de periodos de amortización —n—: Número de periodos que debemos satisfacer la cuota que más adelante vamos a calcular. Siempre en la misma unidad que el tipo de interés.
-
Cuota constante a pagar en cada periodo —α—: La calcularemos con la función PAGO de la hoja de cálculo que tiene la
siguiente estructura: =-PAGO(tasa;nper;va;vf;tipo). Donde:
- Tasa: tanto por uno de interés efectivo correspondiente al periodo en que se pagan las cuotas
- Nper: número de veces que se debe pagar la cuota. O número total de periodos.
- Va: importe del préstamo obtenido.
- Vf: en nuestro caso va a ser siempre 0; pues con la última cuota cancelamos el préstamo.
- Tipo: Puede ser 0 o 1. Como no es objeto de este módulo trabajar con rentas, consideramos que las cuotas se pagan al final de cada periodo, y el valor a utilizar será 0.
- Las comisiones y otros gastos que la entidad financiera percibe por la operación, no van a afectar a los cálculos que realicemos. Pero sí, como veremos al final de la unidad, para determinar el coste financiero de una operación de préstamo.
Autoevaluación
Solución
3.2.- Cálculo de la cuota constante.
El elemento más novedoso y que caracteriza a éste método de amortización es la cuota a pagar en cada periodo. Esta cuota se puede obtener aplicando una fórmula de matemáticas financieras; pero para ello es preciso tener unos mayores conocimientos.
Pero con las hojas de cálculo se simplifica mucho su cálculo. Lo cual no debe significar, en ningún caso, que minimicemos su importancia.
En la imagen siguiente puedes ver cómo hemos calculado la cuota. Analiza la explicación dada en el párrafo anterior con lo que te muestra la imagen. Y además realiza en una hoja de cálculo estos mismos cálculos.
Observa que el tipo de interés y el número de periodos están expresados en la misma unidad de tiempo (meses). Los hemos expresado en meses porque la cuota a pagar es mensual. De tal manera, que será ésta la que determine cómo debemos expresar el tipo de interés y el número de períodos.
Autoevaluación
3.3.- Cálculo de los elementos de un préstamo mediante cuotas constantes.
Ya tenemos todos los datos; por lo tanto veamos cómo utilizarlos para realizar el cuadro de amortización de un préstamo por este sistema de cuotas constantes.
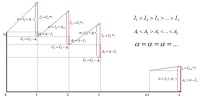
Para complementar la explicación dada con la tabla, te ofrecemos el gráfico que muestra cómo va cambiando cada elemento de periodo a periodo. Analízalo.
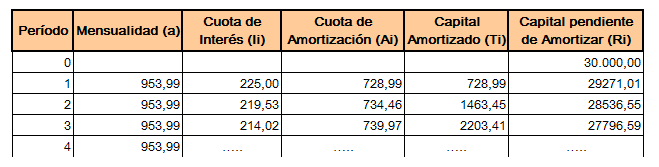
En la imagen siguiente te presentamos:
- Los datos iniciales del préstamo. Incluido el cálculo de la cuota mensual.
- Los cálculos que realizaremos en cada celda del cuadro de amortización. Estúdialos detenidamente hasta que comprendas cómo se calcula cada apartado y, sobretodo, a partir de qué datos.
- Las tres primeras filas del cuadro de amortización; ya resueltas con la explicación anterior.
Debes conocer
Llegado a este punto, te aconsejamos (si estuvieras en un modelo de enseñanza presencial lo haríamos en clase) que realices el cuadro de amortización anterior en una hoja de cálculo.
Para facilitarte su resolución te ofrecemos esta presentación. No obstante, intenta resolver el cuadro de amortización antes de verla.
Pasos para realizar el cuadro de amortización de un préstamo
3.4.- Cálculo del coste financiero de un préstamo.
En un párrafo anterior te comentábamos que de momento no íbamos a tener en cuenta el importe que las entidades financieras cobran en concepto de comisiones. Ahora vas a apreciar cómo debe considerarse para determinar el coste real de un préstamo.
Todos somos conscientes que el coste financiero de un préstamo no está formado sólo por los intereses, sino que debemos tener en cuenta también otros gastos. Recuerdas lo ya estudiado sobre la Tasa Anual Equivalente.
En este apartado vas a recordar la TAE y su uso. Te vamos a indicar cómo aplicarla para determinar el coste financiero de una operación de préstamo.
En el ejemplo utilizado en el apartado anterior presentábamos un préstamo de 30.000 euros por el que nos cobraban una comisión de 450 euros; y por el que debíamos pagar 36 cuotas de 953,99 euros. ¿Qué debemos hacer para calcular la TAE de esta operación?
Volvemos a la hoja de cálculo y diseñamos una columna a la que aplicar la función TIR, con los siguientes valores:
- Capital inicial: -29.550 euros (30.000 que nos han prestado menos 450 euros que hemos pagado de comisión). Ves cómo tenemos en cuenta la comisión: para calcular el coste real.
- A continuación 36 filas con la cuota que pagamos cada mes: 953,99 euros.
- Y después de todas las cuotas: =TIR (celda capital inicial menos comisión : celda última cuota).
- El resultado es un tanto efectivo de 0,8363% mensual. Es decir mayor que el 0,75% que hemos utilizado para resolver el préstamo.
- Por lo tanto la TAE de esta operación es:
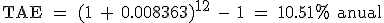
Para saber más
Te proponemos leer el siguiente documento del banco Triodos titulado “Información Precontractual. Préstamo Construcción Vivienda Sostenible”, en el apartado “Vinculaciones y gastos preparatorios”
Autoevaluación
3.5.- Ejercicio resuelto de Préstamo mediante cuotas constantes.
En este apartado vas a realizar el cuadro de amortización de un préstamo, por cuotas constantes, paso a paso. Como en unidades anteriores, te vamos a orientar en la secuencia que hay que seguir; y después de cada paso, una vez que tú lo has resuelto, te ofrecemos la solución. Por ello, es importante, que primero lo resuelvas tú, de tal manera que veas con que operaciones o pasos tienes dificultades. Vamos allá.
Enunciado: Realiza el cuadro de amortización, por el método de cuotas constantes, de un préstamo de 90.000 euros, al 9% anual capitalizable mensualmente, a devolver en 5 años; y cuya comisión de apertura es de 450 €. Una vez finalizado el cuadro de amortización, determina la TAE.
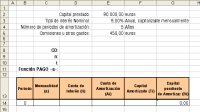
Para realizar el cuadro de amortización te ofrecemos el siguiente fichero: Ejercicio_prestamo.xls.
Formato de hoja de cálculo para resolver el ejercicio.
Ejercicio resuelto
1º. Una vez analizados los datos del préstamo; los debes convertir, si es preciso, para expresarlos en la misma unidad de tiempo. Recuerda debes expresarlos en la unidad de tiempo que se pagan las cuotas (meses, trimestres, ...).
2º. Calcula, mediante la función PAGO, el importe a pagar en cada uno de los periodos de capitalización.
3º. Realiza la línea correspondiente al pago del primer periodo en el siguiente orden:
- Cuota a pagar.
- Cuota de interés.
- Cuota de amortización.
- Capital amortizado.
- Capital pendiente de amortizar.
4º. Confecciona la línea correspondiente al segundo periodo. El valor de cada celda lo obtenemos a partir de los datos calculados con anterioridad. De tal manera que copiando esta línea hacia abajo, completamos el cuadro.
5ª. Una vez realizado el cuadro completo, procede a determinar la TAE.
4.- Otros servicios bancarios.
Caso práctico

 -Ahora sí que hemos logrado
completar toda la documentación que nos propusimos; le dice Pilar a Jorge.
-Ahora sí que hemos logrado
completar toda la documentación que nos propusimos; le dice Pilar a Jorge.
Jorge se muestra satisfecho. Cree que ha merecido la pena el esfuerzo realizado. Y se siente con suficiente seguridad como para llevar a cabo diversas operaciones bancarias.
Pilar comparte esta sensación. Y le apunta que ahora ya no hace falta acudir a las oficinas bancarias para realizar algunas operaciones. Pues se pueden llevar a cabo desde la propia empresa, con un ordenador y conexión a Internet.
4.1.- Servicios bancarios on-line.
 Las nuevas tecnologías nos están cambiando no sólo las formas de relacionarnos, sino también los hábitos diarios: comprar, buscar información de cualquier tipo, leer los periódicos,... Y cómo no, la manera de realizar las operaciones financieras.
Las nuevas tecnologías nos están cambiando no sólo las formas de relacionarnos, sino también los hábitos diarios: comprar, buscar información de cualquier tipo, leer los periódicos,... Y cómo no, la manera de realizar las operaciones financieras.
Posiblemente tú ya realizas algunas operaciones (comprobar el saldo de las cuentas; realizar transferencias; consultar los cargos de tu cuenta;...) a través de un ordenador con conexión a Internet. Es lo que se conoce como banca on-line; o banca por Internet.
Con este apartado pretendemos, por una parte, resaltar la importancia que este sistema ha alcanzado, y que en el futuro ampliará sus posibilidades; y por otra, analizar brevemente su funcionamiento.
La gran mayoría de las entidades financieras ofrecen servicios online a sus clientes. Para que éstos puedan utilizarlos, les proporcionan un nombre de usuario y una contraseña. De tal manera que se facilita la realización de la mayor parte de las operaciones, sin necesidad de acercarse a la oficina.
Como ventajas podemos enumerar:
- El ahorro de tiempo que supone el realizar las operaciones desde el propio domicilio o el puesto de trabajo.
- La comodidad y rapidez con la que se realizan las operaciones.
- Se realizan mediante conexiones protegidas por eficaces sistemas de seguridad. Pensemos que el éxito de esta manera de operar se basa en la confianza de los clientes en la misma; por ello se adoptan diversas medidas para garantizar la privacidad y la seguridad del cliente.
Como desventajas apuntamos:
- Se trata de un sistema que todavía no permite realizar todas las operaciones.
- Aunque la extensión del uso de Internet es amplísima; todavía hay muchas personas que desconfían de este medio. Y vencer esta resistencia, así como lograr que la gran mayoría de la población sepa utilizarlo, llevará su tiempo.
- Se pierde el contacto personal que, para realizar estas algunas operaciones, es importante.
Por último, sin pretender ser exhaustivos, las operaciones se suelen realizar con este sistema son:
- consultas de: saldo de las cuentas; movimientos de las mismas; pagos realizados; ...
- realizar transferencias: entre cuentas propias o ajenas; periódicas o puntuales; ...
- domiciliar recibos.
- contratar nuevos productos: depósitos; fondos de inversión; ...
- hacer uso de un buzón virtual para comunicaciones con la entidad financiera.
- ...
Autoevaluación
Indica si son verdaderas o falsas cada una de las siguientes afirmaciones:
Retroalimentación
Falso
Todo lo contrario; es una ventaja.Retroalimentación
Verdadero
En algunos casos es la ventaja más valorada.Retroalimentación
Falso
Todavía hay muchas personas que, por diversas razones, no confían en este sistema.Retroalimentación
Verdadero
Sobre todo para las personas mayores; y cuando hay que negociar operaciones.Anexo.- Licencias de recursos.
| Recurso (1) | Datos del recurso (1) | Recurso (2) | Datos del recurso (2) |
|---|---|---|---|
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Latinstock. Licencia: Uso educativo para plataformas públicas de FPaD. Procedencia: Latinstock. |
 |
Autoría: Banca online Licencia: Copyright(cita). Procedencia: https:/www.beltiberica.sa.es |