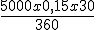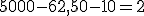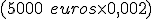Valoración de los productos y servicios financieros.

Todas las empresas trabajan con diferentes productos y servicios financieros. En nuestro caso, Andalucía Vende dispone de diversas cuentas corrientes y cuentas de ahorro en varias entidades financieras. Las empresas suelen trabajar con diferentes entidades financieras por varios motivos, como por ejemplo, diversificar el riesgo, tener más posibilidad de acceder a diferentes productos, etc.
Luna va a empezar a trabajar con los productos financieros que tiene contratados Andalucía Vende con sus diferentes entidades financieras. Se le va a proporcionar documentos relativos a cuentas corrientes, cuentas de ahorro, préstamos, depósitos u operaciones de leasing.
Carmen se reúne con Luna y le informa que los datos que la empresa le va a suministrar son de una gran importancia y le pide los trate la cautela y prudencia que requieren. Luna es perfectamente consciente de la importancia que va a suponer para ella este paso en su formación, además de la responsabilidad que la empresa deposita en ella. Carmen le indica a Luna que la empresa va a apostar por ella, por haber realizado un gran trabajo en estas últimas semanas.
En esta fase de la formación, será Carmen la encargada de tutorizar personalmente a Luna.
El plan de formación que Carmen ha preparado para Luna buscará dar respuesta a las siguientes cuestiones:

- ¿Cómo se realiza el análisis y el cálculo de las operaciones de descuento de efectos?
- ¿Cómo se realiza el análisis y el cálculo de las líneas de crédito?
- ¿Cómo se realiza el análisis y el cálculo de las liquidaciones de cuentas?
- ¿Cómo se realiza el análisis y el cálculo de las operaciones de depósitos?
- ¿Cómo se realiza el análisis y el cálculo de las operaciones de préstamos?
- ¿Cómo se realiza el análisis y el cálculo de las operaciones de arrendamiento financiero?
- ¿Cómo se realiza el análisis y el cálculo de las operaciones de empréstitos?
- ¿Cómo utilizar la hoja de cálculo en el análisis y valoración de los productos financieros?

1.- Análisis de las operaciones de descuento de efectos y líneas de crédito.

Luna va a comenzar con la formación que le ha propuesto Carmen sobre el análisis y la valoración de los distintos productos y servicios financieros. Va a comenzar analizando dos tipos de operaciones muy comunes en el desarrollo diario de cualquier empresa, nos referimos a las operaciones de descuento de efectos y a las líneas de crédito.
En las unidades anteriores has aprendido que, tanto los descuentos de efectos como los créditos, son dos elementos fundamentales a través de los cuales las empresas consiguen obtener recursos con los que financiar su actividad. Se tratan de operaciones financieras de corto plazo, pero:
- ¿Cómo funcionan en la práctica?
- ¿Cómo se realiza su cálculo?
En este apartado vas a dar respuesta a estas dos preguntas. Para ello vas a aprender a realizar e interpretar las operaciones de cálculo, aprender las fórmulas necesarias y a aplicarlas en ejercicios prácticos.
1.1.- Análisis de las operaciones de descuento de efectos.

Imagina que tu empresa realiza una gran venta de productos a un cliente. El cliente te paga mediante un título de crédito a 90 días (por ejemplo mediante una letra o un pagaré), pero se trata de una cantidad muy importante de dinero y en ese momento, en tu empresa, no hay suficiente liquidez como para poder afrontar el pago de las nóminas del mes a tus trabajadores, en este contexto, necesitas dinero urgentemente, ¿Qué puedes hacer? La solución en el corto plazo (que es lo que se requiere para este caso) sería llevar el título de crédito al descuento.
Mediante esta operación, tu empresa obtendrá por adelantado la cantidad de la venta, pero ¿recibirá íntegramente la cantidad documentada en el título de crédito? Como ya pudiste estudiar en unidades anteriores la respuesta a esta pregunta es no, ya que el banco descuenta de esa cantidad una serie de comisiones e intereses.
Para realizar el cálculo utilizaremos los conceptos que se recogen en la siguiente tabla:
| Elementos | Descripción | Cálculo |
|---|---|---|
| Efectivo o líquido. | Importe anticipado por la entidad a su cliente (empresa que presenta el título de crédito). |
Se calcula restando del importe de la letra (nominal) el importe de todos los costes originados por el descuento (intereses, comisiones y otros gastos).
Donde, N: nominal del efecto. I: intereses. C: comisiones. Se aplica sobre el nominal. G: otros gastos. |
| Intereses. | Cantidad cobrada por la anticipación del importe de la letra. |
Donde: N: nominal del efecto. d: tipo de descuento anual (en tanto por uno). t: número de días que el banco anticipa el dinero. |
| Comisiones. | Cantidad que cobra la entidad financiera como consecuencia del riesgo asumido. Normalmente es un porcentaje aplicable al nominal con una cantidad mínima. | Se trata de una cantidad impuesta por la entidad financiera y que debemos negociar con ella para intentar siempre rebajarla. |
| Otros gastos. | Se denominan suplidos, y suelen incluirse conceptos como por ejemplo el timbre, la comisión por negociación, o la comisión por gestión de cobro. | Es muy importante que en el acuerdo con la entidad financiera queden claros todos los gastos que nos aplicarán en estas operaciones. |
A continuación vas a practicar lo aprendido con el siguiente ejemplo:
La empresa Andalucía Vende desea descontar una letra de 5.000€. Aún faltan 30 días para su vencimiento. Las condiciones que la empresa tiene contratadas con la entidad financiera son las siguientes:
- Tipo del descuento: 15%.
- Comisión: 0,2% (mínimo de 5€).
- Otros gastos: 2€.
| Elementos | Resultado |
|---|---|
| Nominal. | 5.000 €. |
|
Intereses.
|
62,50 €. |
|
Comisión.
|
10 €. |
| Otros gastos. | 2 €. |
|
Efectivo.
|
4.925,5 €. |
1.1.1.- Letra devuelta.

Siguiendo con el ejemplo anterior, imagina ahora que llegado el vencimiento de la letra (es decir, han pasado los 30 días que faltan para el cobro), la entidad financiera se dirige al librado para cobrársela, pero éste no atiende al pago, ¿qué ocurrirá ahora? Recuerda que la entidad financiera ya nos había adelantado el dinero.
En este caso la entidad financiera cargará a Andalucía Vende el importe de la letra no atendida por el librado además de una serie de gastos que se han originado por el impago. Entre estos gastos destacamos:
- Gastos de devolución.
- Comisiones de devolución.
- Correo.
- Gastos de protesto.
- Comisión de protesto.
- Coste del protesto.
- Intereses.
Cuando la entidad financiera cobre el importe de la letra con posterioridad a la fecha de vencimiento se calcularán sobre la suma del nominal de la letra impagada más el importe de todos los gastos originados por el impago, por el periodo transcurrido entre el vencimiento y el cargo.
Continuando con el ejemplo anterior, llegado el vencimiento de la letra, el cliente de Andalucía Vende no atiende el pago de la letra a la entidad financiera. En este momento, el banco se dirige a Andalucía Vende cargándole en cuenta los siguientes conceptos:
- Comisión de devolución: 0,1 %.
- Comisión de protesto: 0,2 %.
- Correo: 2,50 €.
| Elementos | Resultado |
|---|---|
| Nominal. | 5.000 €. |
|
Comisión de devolución. |
5 €. |
|
Comisión de protesto. |
10 €. |
| Correo. | 2,5 €. |
| Total gastos. | 17,5 €. |
| Adeudo en la cuente de Andalucía Vende S.L. | 5.017,5 €. |
1.1.2.- Letra de resaca o devolución.

Imagina ahora que una vez que la letra ha no ha sido pagada por el librado (tal y como había ocurrido en el caso anterior), tu empresa emite otra letra para intentar recuperar la letra que no fue pagada por tu cliente. En este caso tenemos que ver cuál será ahora el nominal de la nueva letra, ya que el impago te generó una serie de gastos que ahora debes recuperar.
Para realizar el cálculo deberemos actuar como con cualquier letra que se emite y se lleva al descuento, pero con una particularidad, en este caso el efectivo (cantidad que deseamos recuperar formada por el nominal más los gastos ocasionados del impago) es conocido, mientras que el nominal es desconocido, y por lo tanto, deberemos calcularlo.
Continuando con el ejercicio anterior, Andalucía Vende negocia con su cliente (el librado) y negocian una nueva letra, asegurando el librado que hará frente a ella. En este momento se gira una nueva letra a 60 días con las siguientes condiciones:
- Tipo de descuento: 16 %.
- Comisión: 0,4 % con un mínimo de 5 €.
- Otros gastos: 15 €.
El efectivo sabemos que tiene que ser el nominal más los gastos ocasionados por el impago: 5.017,5€. Esta cantidad es la calculada en el apartado anterior.
Por otro lado, sabemos que:
![]()
![]()
Sustituyendo:
![]()
![]()
![]()
![]()
![]()
El nominal del efecto debe ser de 5.193,50 € para que el efectivo adelantado por la entidad financiera sea la cantidad del primer efecto incluido los gastos que le ocasionó el librado a la empresa por su impago.
1.1.3.- Descuento de una remesa de efectos.

En la práctica real, lo normal es que te encuentres con una cantidad de efectos para descontar, denominándose a este proceso el descuento de una remesa de efectos. Estos efectos que se llevan de forma conjunta tienen diferentes períodos de tiempo, unos por ejemplo, estarán emitidos a 30 días, otros a 60 días, y así sucesivamente. Las entidades financieras agrupan los efectos en función a esos periodos de tiempo para realizar el cálculo y aplicar las condiciones previamente pactadas del descuento. Igualmente tienes que tener muy presente que las entidades financieras ofrecen a sus clientes una línea de descuento, es decir, un límite máximo de cantidad de recibos a descontar. Se trata de un límite que deberás negociar con tu banco.
La entidad financiera llevará al descuento la remesa y pasará a su cliente la llamada factura de negociación, en la cual se detallan todos los efectos que componen la remesa. El proceso es el que se detalla a continuación:
- Se confecciona la factura de negociación con todos los efectos que formarán la remesa (agrupados en función a su periodo de tiempo).
- Se suma cada uno de los siguientes conceptos:
- Importe nominal.
- Importe de los intereses.
- Importe de las comisiones.
- En caso de existir gastos como por ejemplo de correo, timbres, etc. sus importes se suman aparte de los anteriores conceptos.
- El importe líquido resultante de la negociación se obtendrá restante del nominal total de la remesa la suma de todos los gastos que se hayan producido.
A continuación seguiremos con el ejemplo de la empresa Andalucía Vende, la cual presenta a su entidad financiera la siguiente remesa de efectos.
| Efecto | Importe nominal | Días de descuento |
|---|---|---|
| Efecto A. | 20.000 €. | 15. |
| Efecto B. | 15.000 €. | 25. |
| Efecto C. | 10.000 €. | 30. |
Las condiciones del descuento negociadas con la entidad financiera son las siguientes:
- Tipo de descuento: 15 %.
- Comisión: 0,4 % con un mínimo de 60 €.
- Correo: 5 €.
| Efecto (E) | Nominal (N) | Días (t) | Tipo de descuento (d) |
Intereses
|
Tipo de comisión (c) |
Comisión
|
Correo (G) |
|---|---|---|---|---|---|---|---|
| A. | 20.000 €. | 15. | 15 %. | 125 €. | 0,4 %. | 80 €. | 5 €. |
| B. | 15.000 €. | 25. | 15 %. | 156,25 €. | 0,4 %. | 60 €. | 5 €. |
| C. | 10.000 €. | 30. | 15 %. | 125 €. | mínimo. | 60 €. | 5 €. |
| Sumas. | 45.000 €. | 406,25 €. | 200 €. | 15 €. |
Ahora calculamos el total del efectivo recibido:
| Valor nominal de la remesa | 45.000 €. |
|---|---|
| Intereses | 406,25 €. |
| Comisiones | 200 €. |
| Correo | 15 €. |
| Total gastos | 621,25 €. |
| Efectivo recibido | 44.378,75 €. |
1.2.- Análisis de las operaciones de líneas de crédito.

En este punto vas a aprender a realizar los cálculos necesarios para realizar el análisis de las operaciones de crédito que realizan las empresas. Las empresas suelen tener, al menos, una línea de crédito (también conocida como póliza de crédito) con la que financiarse a corto plazo, disponiendo de un medio de financiación con el que poder afrontar los pagos de la actividad ordinaria de la empresa.
La utilización de una póliza de crédito lleva aparejados una serie de costes para la empresa que necesitamos conocer para poder realizar el análisis de las operaciones de crédito:
- Intereses: que son calculados sobre los saldos vigentes, en función del tiempo de vigencia y del tipo contratado.
- Intereses deudores: aplicados a la parte de crédito que se haya dispuesto.
- Intereses excedidos: aplicados a la parte dispuesta que excede del límite del crédito acordado.
- Comisión de apertura: que estará en función al límite del crédito concedido. Es pagadera una vez y al principio de la operación.
- Comisión de disponibilidad: que irá en función al saldo medio no dispuesto, es decir, es lo que hay que pagar por la parte del crédito contratado y no dispuesto.
- Comisión por excedido: se aplica sobre el mayor saldo excedido o parte utilizada que está por encima del límite del crédito.
El procedimiento a seguir en la liquidación de una cuenta de crédito queda recogido en el siguiente cuadro:
| Fases | Cálculo |
|---|---|
| 1ª | Cálculo del saldo de la cuenta cada vez que se realiza un nuevo movimiento. |
| 2ª | Calcular los días que cada saldo está vigente. |
| 3ª | Cálculo de los números comerciales, multiplicando cada saldo por los días que está vigente, clasificando los números en: deudores, excedidos y acreedores según sean sus saldos. |
| 4ª | Realizar la suma de los números deudores, excedidos y acreedores. |
| 5ª |
Realizar el cálculo de los intereses:
|
| 6ª |
Realizar el cálculo de las comisiones sobre saldo medio no dispuesto:
El resultado se cargará en cuenta. |
| 7ª | Realizar el cálculo sobre la comisión por el saldo excedido. |
| 8ª | Calcular el saldo de la cuenta mediante la diferencia entre el debe y el haber. |
Documento que muestra la liquidación de una cuenta de crédito que tiene firmada Andalucía Vende con su entidad financiera. En este ejemplo vas a practicar con la elaboración de un cuadro de liquidación y con las operaciones de cálculo necesarias para la determinación de dicha liquidación.
1.3.- Aplicación financiera de la hoja de cálculo.

A lo largo de tu vida profesional y personal tendrás que utilizar muy asiduamente las nuevas tecnologías. Estas tecnologías han sido creadas para hacerte más fácil tú día a día. Si nos centramos en el ámbito profesional, la utilización de las nuevas tecnologías te ha de facilitar el desempeño de tú trabajo, contribuyendo a aumentar tú eficiencia. Un claro ejemplo de estas herramientas tecnológicas son las hojas de cálculo, a través de las cuales puedes realizar cálculos complejos de una manera sencilla disminuyendo el tiempo empleado en dichas operaciones de cálculo.
A través del siguiente vídeo puedes ver que se explica detalladamente cómo realizar la liquidación de una póliza de crédito mediante la utilización de la hoja de cálculo.
2.- Operaciones con cuentas corrientes.

Luna ha aprendido a realizar el cálculo y análisis de las operaciones con pólizas de crédito. A partir de ahora se centrará de las operaciones con las cuentas corrientes. En este momento a Luna le encargan cotejar los documentos relativos a las cuentas corrientes de la empresa, su trabajo consistirá en comprobar que los movimientos de las cuentas corrientes son correctos y deberá controlar el saldo de dinero disponible en ellas. Se trata de un trabajo de gran importancia, en realidad, cualquier trabajo que implique controlar el dinero de la empresa requiere gran destreza, conocimiento y sobretodo atención.
Todos los usuarios, ya sean empresas o particulares, disponemos de cuentas corrientes donde ingresamos y retiramos efectivo. A través de las cuentas realizamos pagos (como los pagos domiciliados correspondientes a recibos de luz, agua, teléfono, etc.) e ingresos (aportaciones propias, cobros de clientes, domiciliaciones de letras, etc.), pero ¿alguna vez de te has preguntado cómo funcionan en realidad?
Las cuentas corrientes siguen una numeración que está normalizada desde 1979, en el que se establece el Código de Cuenta Cliente (CCC) y cuya estructura se explica en el siguiente cuadro:
| Entidad (4 dígitos) | Oficina (4 dígitos) | Dígitos de control (2 dígitos) | Número de cuenta (10 Dígitos) |
|---|---|---|---|
| 0123 | 0345 | 10 | 100055668975 |
Las anotaciones en las cuentas son de dos tipos:
- Ingresos: el cliente realiza operaciones de ingresos en efectivo, transferencias a favor, cobros de letras, pagarés o cheques, etc. La entidad financiera anotará una operación de débito o abono a favor del cliente. Debe aparecer en el haber de la cuenta corriente.
- Reintegros: el cliente retirará efectivo mediante tarjetas, personalmente en la entidad bancaria, se realizarán pagos por domiciliaciones de recibos, impuestos, etc. La entidad anotará una operación de adeudo o cargo al cliente. Debe aparecer en el debe de la cuenta corriente.
- Método directo: este método considera que cada capital (deudor o acreedor) devenga intereses durante los días que van desde la fecha de su vencimiento hasta el momento de la liquidación.
- Método indirecto: este método consiste en que los capitales generan intereses desde la fecha en la que se originan hasta una fecha denominada época, lo que implica un cálculo de intereses que no se corresponde con la realidad, ya que cuando se conozca la fecha de liquidación deberán de rectificarse y actualizarse.
- Método hamburgués o de saldos: recibe este nombre porque se realizó por primera vez en Hamburgo, y de saldo porque los números comerciales se calculan en base a los saldos que van apareciendo en la cuenta (no en función a los capitales). En el siguiente punto vas aprender a realizar la liquidación de una cuenta corriente mediante el método hamburgués (que es el empleado por las entidades financiera en las operaciones de liquidación de cuentas corrientes).
2.1.- Operación de liquidación de cuentas. Método hamburgués.
A continuación vas a aprender a operar con cuentas corrientes y a entender su funcionamiento.
En primer lugar es necesario que conozcas los elementos y la terminología que intervienen en las cuentas corrientes, que son necesarios para su cálculo y análisis. Todos estos elementos y definiciones quedan recogidos de forma esquemática en el siguiente cuadro:

| Elementos | Detalle |
|---|---|
| Fecha de apertura. | Día de formalización del contrato. |
| Vencimiento de un capital o fecha valor. | Día en el que el capital comienza a generar intereses. |
| Los pagos y cargos se valoran el mismo día. | Se valoran el mismo día que se cumplimenta la operación. |
| Recuento de los días. | Se deben contar las fechas utilizando los días, meses y años naturales. |
| Fecha de liquidación. | Día en el que se liquida la cuenta y se toma para el cálculo de los intereses de la cuenta y el saldo correspondiente. |
| Saldo. | Diferencia entre la suma de las partidas deudoras y la suma de las partidas acreedoras. |
| Tipo de interés. | Se aplica a los capitales anotados en cuenta. Puede existir un mismo tipo de interés para saldos deudores y acreedores (cuentas corrientes de interés recíproco) o distinto tipo de interés (cuentas corrientes de interés no recíproco). |
| Capital. | Importe monetario de la operación. |
| Descubierto en cuenta corriente o números rojos. | Cuando la cuenta tiene un saldo deudor a favor de la entidad financiera porque se ha dispuesto una cantidad superior al saldo acreedor. Se aplicará una comisión. |
El primer paso para valorar una cuenta bancaria es adjudicarle una fecha para poder realizar el cálculo de los intereses. En este sentido tienes que diferenciar entre la fecha donde tiene lugar la operación (fecha de la operación) y la fecha que se considerará para el cómputo de los intereses (fecha valor).
La Circular 8/1990, de 7 de septiembre, del Banco de España establece las condiciones mínimas de valoración que deben aplicar las entidades financieras, distinguiendo entre operaciones de abono y de adeudo. La información puedes verla en los anexos de la Circular.
Los pasos a seguir se resumen en el siguiente cuadro:
| Fases | Cálculo |
|---|---|
| 1ª | Ordenar las operaciones según su fecha valor. |
| 2ª | Calcular las operaciones de saldos como diferencia entre el Debe y el Haber. Ten en cuenta que cada vez que se realice un movimiento cambiará el saldo de la cuenta. |
| 3ª | Calcular los días de vencimiento a vencimiento, y del último vencimiento a la fecha de cierre. |
| 4ª | Calcular los números comerciales multiplicando los saldos por los días y se colocan en el Debe, si el saldo es deudor, o en el Haber si es saldo es acreedor. |
| 5ª |
A continuación procederemos a la liquidación de la cuenta:
|
- A continuación realizaremos un ejercicio sobre la liquidación de una cuenta corriente que tiene firmada Andalucía Vende con su entidad financiera. En este documento se presenta de forma fácil y comentada cada una de las fases que tienes que realizar a la hora de realizar la liquidación de una cuenta corriente.
- En el siguiente enlace puedes descargar otro ejemplo de liquidación de una cuenta corriente. Al igual que en el caso anterior, se trata de un ejercicio en el que se presenta de forma clara y detallada todas las operaciones a seguir en el caso de la liquidación de una cuenta corriente. La particularidad de este ejercicio es que en dicha liquidación aparecen descubiertos en la cuenta.
2.2.- Aplicación financiera de la hoja de cálculo.

A lo largo de tu vida profesional y personal tendrás que utilizar muy asiduamente las nuevas tecnologías. Estas tecnologías han sido creadas para hacerte más fácil tú día a día. Si nos centramos en el ámbito profesional, la utilización de las nuevas tecnologías te ha de facilitar el desempeño de tú trabajo, contribuyendo a aumentar tú eficiencia. Un claro ejemplo de estas herramientas tecnológicas son las hojas de cálculo, a través de las cuales puedes realizar cálculos complejos de una manera sencilla disminuyendo el tiempo empleado en dichas operaciones cálculo.
La hoja de cálculo debe ser una herramienta más que debes utilizar en tu trabajo, como lo es también el teléfono móvil, el ordenador, la agenda, etc.
En el siguiente vídeo puedes ver como se realiza el cálculo de la liquidación de cuentas corrientes a través del método hamburgués mediante la hoja de cálculo.
3.- Análisis de las operaciones de depósitos.
En la formación que está realizando Luna sobre la valoración de los productos y servicios financieros, ha aprendido a trabajar con las cuentas corrientes y con las operaciones de descuento de efectos. Se trata de dos tipos de operaciones muy comunes en el día a día de las empresas. Luna está comprobando como aplicar los conceptos teóricos a la realidad empresarial, lo cual le está ayudando mucho a comprender el funcionamiento de la empresa. Rafael y Carlos no se separan de ella y la asesoran en todo momento, ya que esta parte de la formación requiere mucha destreza y concentración, debido a que está trabajando con la gasolina de la empresa, es decir, con el dinero que mueve la organización.
Al salir de la empresa, Luna queda con su amiga Marta para tomar café. Marta se interesa por las prácticas de Luna y ésta le cuenta que está realizando operaciones relativas a la valoración de cuentas corrientes y descuentos de efectos. En los próximos días comenzará a trabajar con las operaciones de depósitos. Marta le dice que ella tiene un dinero en una cuenta corriente y que su entidad financiera le ha ofrecido un depósito pero no sabe qué hacer. Marta le dice que se informe de todas las características del depósito para así enseñarle como calcular la rentabilidad que obtendría por esa inversión.


Tienes que tener muy claro que las empresas no pueden, o mejor dicho, no deben tener el dinero retenido, es decir, que han de mover o invertir el dinero con el objetivo de obtener una rentabilidad, un beneficio. Si una empresa no cumple con este principio básico de las finanzas, estará teniendo un coste de oportunidad muy elevado y dejará de obtener unas rentabilidades que puede necesitar en un futuro.
Las empresas invierten sus excesos de tesorería en diferentes productos financieros que puede encontrar en el mercado financiero. Igualmente, los particulares, como puede ser tu caso, cuando disponen de una cantidad de dinero importante y que no van a utilizarla durante tiempo, optan por buscar alternativas que les genere un rendimiento durante ese tiempo que no necesitarán dichos recursos económicos.
Una alternativa a los excesos de tesorería o liquidez que acabamos de comentar son los denominados depósitos o imposiciones a plazo fijo, que ya has estudiado en la unidad anterior. Ahora es el momento de afrontar el estudio del cálculo y análisis de estos productos financieros.
3.1.- Operaciones de depósitos.

En este apartado vas a aprender a trabajar con depósitos o imposiciones a plazo. Se trata de un producto financiero muy común y muy demandado por las unidades con superávit o ahorradoras, ya sean empresas o particulares.
Las operaciones de depósitos son sencillas, si bien es cierto que hay algunos aspectos a tener muy en cuenta. Cuando vas a una entidad financiera a preguntar por los diferentes depósitos o imposiciones a plazo que tienen, te darán tres datos:
- Uno referido al tiempo de la imposición. Existen depósitos a tres, seis, doce y dieciocho meses. Por encima de esos plazos también se ofrecen depósitos, pero los más comunes se mueven entre esos plazos. Igualmente podrás apreciar que entre unos y otros existen diferencias, que incluso, llegan a ser bastante significativas.
- Otro al periodo de liquidación de intereses. En lo referente al periodo de liquidación de los intereses, éstos se suelen abonar de forma trimestral, semestral o anual, en otros casos, se indica que el abono de los intereses en la cuenta del cliente se realizará mediante un único pago al finalizar la imposición. Éste es otro dato a tener en cuenta a la hora de optar por unos u otros.
- Y otro referente al tipo de interés. En este punto nos detendremos un poco. Cuando te dirijas a una entidad financiera para preguntar por los depósitos te indicarán el tipo de depósito (normalmente tienen denominaciones llamativas) y te comentarán dos tipos de interés, el nominal y la TAE.
Cuando te indican ambos tipos de interés, la TAE suele ser superior al interés nominal (aunque en ocasiones es el mismo), esto es debido a que la TAE incluye, además del tipo de interés, las comisiones y el plazo de la operación. Se trata, por lo tanto, de un interés más real y exacto que el interés nominal que no incluye esas variables. La TAE recoge el rendimiento que realmente vamos a recibir por nuestro dinero e incluye todas las liquidaciones de pago que nos vayan haciendo adelantadamente.
La fórmula de la TAE es la siguiente:
Siendo:
i: tipo de interés nominal.
m: frecuencia de cobro o pago.
k: frecuencia de cobro o pago.
Veamos un ejemplo:
Si invertimos 10.000€ en un depósito mensual y nos dicen que nos dan una TAE anual del 7%, resultará que realmente nos están dando:
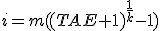 =
=Es decir, el tipo de interés nominal anual es del 6,785%, y al mes nos darán realmente:
![]()
Como conclusión, siempre que vayas a pedir información sobre varios productos financieros, aunque tengan diferentes vencimientos, para poder compararlos, debes utilizar la TAE de cada uno de los productos.
A través de este a la web del Banco de España vas a poder realizar una simulación del cálculo de la TAE que te permitirá calcular el importe de los intereses brutos a percibir en un depósito bancario, con un Tipo de Interés, plazo y periodicidad de pago determinados, calculando además su Tasa Anual Equivalente.
3.2.- Depósitos estructurados.

Si has estado en una entidad financiera últimamente para preguntar por los depósitos que tienen para invertir un dinero con el fin de obtener una rentabilidad, seguro que te ha ofrecido un depósito estructurado (indexado). En la unidad anterior ya estudiaste las principales características de los depósitos estructurados o también llamados depósitos diversificados o depósitos combinados.
Retomando lo estudiado en la unidad anterior, estos depósitos consisten en dividir la cantidad impuesta en dos, una parte es destinada a un depósito a plazo fijo, y la otra es invertida en unos valores de referencia, normalmente se trata de valores bursátiles (acciones de empresas muy importantes y que cotizan en el IBEX 35). La rentabilidad está ligada a que esos valores aumenten (TODOS) en unas fechas determinadas, o en su caso, a que la media de las valoraciones del valor bursátil sea mayor a la valoración de referencia. Veamos un ejemplo:
Andalucía Vende realiza una imposición en un depósito estructurado de 30.000€ el 5 de Marzo de 2012, el cual se dividirá en dos tramos. Las características del depósito son las siguientes:
- Tramo 1: el 70 % de la inversión consistirá en una imposición a 6 meses que remunera a su vencimiento (5 de Septiembre de 2012) un interés nominal anual del 4,451 % (TAE 4,50 %).
- Tramo 2: el 30 % de la inversión consistirá en una imposición a 36 meses que remunera a su vencimiento (5 de Marzo de 2015) una rentabilidad equivalente al 50 % de la revalorización media mensual de la cotización de un valor del IBEX-35 (Telefónica) con una rentabilidad mínima del 1 % (TAE 0,33 %).
- Referencia inicial: mayor precio de cierre de la acción desde el 5 de Marzo de 2012 al 5 de Abril de 2012, ambos inclusive. Suponemos que el valor de referencia es de 13,40 €.
Vamos a calcular el rendimiento de la inversión:
| Primer tramo. Inversión del 70 % que corresponde a 21.000 € | |
|---|---|
| Cálculo de la rentabilidad (intereses). |
Los intereses brutos obtenidos son de 1.471,20 €. |
| Segundo tramo. Inversión del 30 % que corresponde a 9.000 €. | |
| Calculo de la rentabilidad para el caso en el que la cotización de las acciones de telefónica sea superior al valor de referencia inicial. |
Suponemos que la media de las 36 observaciones es de 17,98:
Los intereses brutos obtenidos son de 1.538,06 €. |
| Calculo de la rentabilidad para el caso en el que la cotización de las acciones de telefónica sea inferior al valor de referencia inicial. |
En este caso, supongamos que la media de las 36 observaciones es inferior al valor de referencia, por ejemplo del 12,5 %. En este caso la revalorización sería negativa, por lo tanto, según la información del producto, se le aplicaría una rentabilidad adicional del 1 %:
Los intereses brutos obtenidos son de 90,00 €. |
4.- Análisis de préstamos.

Carlos está muy contento con el trabajo de Luna, y así se lo hace saber a Carmen. Hasta ahora, Luna ha realizado correctamente las operaciones que le propuso Carmen en su plan de formación.
A partir de ahora, Luna va a comenzar a trabajar con los préstamos. Carlos le muestra los distintos préstamos que tiene Andalucía Vende con varias entidades financieras y le muestra las características de cada uno. A continuación, Carlos le indica que la empresa tiene previsto realizar nuevas inversiones para las cuales buscará financiación a través de un préstamo. Luna deberá analizar las diferentes alternativas que le han propuesto las entidades financieras. Se trata de un trabajo que implica una gran responsabilidad, pero Luna se siente perfectamente capaz, tiene mucha confianza en sí misma y en sus compañeros, los cuales le ayudarán ante cualquier duda que le surja.

Ya has estudiado en unidades anteriores en qué consisten los préstamos. Ahora te centrarás en su valoración y liquidación. Para poder realizar el cálculo de la amortización de un préstamo, necesitas conocer qué variables intervienen en el cálculo. Posteriormente te introducirás en el cálculo de los diferentes métodos de amortización de préstamo.
Al igual que en los casos anteriores, se trata de una parte muy práctica, para lo cual es necesario que prestes la mayor atención y realices los cálculo en tu bloc de notas a la vez que los veas en pantalla.
4.1.- Variables que intervienen en el cálculo.
Para comenzar a realizar operaciones de cálculo con los préstamos, necesitas conocer las diferentes variables que intervienen en su cálculo, para ello vamos a utilizar la siguiente tabla:
| Variables | Detalle |
|---|---|
| Capital vivo. | Es la cuantía de la deuda pendiente de amortizar en un momento determinado (k). |
| Anualidad. |
Es el pago que ha el prestatario con el fin de amortizar el préstamo. Está formado por la cuota de amortización más la cuota de interés:
|
| Cuota de amortización. |
Es la cantidad amortizada en un periodo k.
|
| Cuota de interés. |
Es la cantidad de intereses que se pagan por el capital vivo o pendiente.
|
| Tasa de interés efectiva. | Es el tipo de interés que se aplica para calcular la cuota de interés. |
| TAE. | Es el tipo de interés teniendo en cuenta las comisiones y gastos del préstamo. Si no aplica esos gastos, coincidirá con la tasa anual efectiva (i). |
| Tanto nominal. | Es un tipo de interés que indican habitualmente las entidades para la concesión de préstamos o realización de depósitos. Se identifica como tanto nominal capitalizado en periodos fraccionados inferiores a un año. |
| Tiempo o duración. | Es la duración del préstamo (n). |
| Comisiones y gastos. | Consisten en la comisión de apertura, la comisión por cancelación total o parcial, etc. |
| Cuadro de amortización. |
Es la forma de presentar cada uno de los pasos que tiene el pago de un préstamo en cada periodo y en el que se indican:
|

A continuación va a realizar el cálculo de la amortización de un préstamo, para ello, vas a realizar el cálculo mediante cuatro procedimientos:
- Amortización por el sistema americano.
- Amortización por el sistema francés.
- Amortización por el sistema alemán.
Para realizar el cuadro de amortización utilizaremos el siguiente modelo:
| Períodos | Término amortizativo | Cuota de interés | Cuota de amortización | Total Amortizado | Capital vivo |
|---|---|---|---|---|---|
|
0 1 2 ... n |
- a1 a2 |
- I1=C0 xi1 I2=C1xi2 |
- A1=a1- I1 A2=a2- I2 |
- m1=A1 m2=A1+A2 |
- C0 C1=C0-A1 C2=C0-A1-A2 |
4.2.- Amortización por el sistema americano.

El método de amortización por el sistema americano se caracteriza porque durante el periodo del préstamo, el prestatario satisface en cada fecha de vencimiento los intereses (C x i), a una tasa de interés efectiva anual (i), reembolsando mediante un único pago (C) el capital que recibió como préstamo al término del año (n).
a1=a2=a3=...=an-1=C0 x i
an=Co + Co x i
I1=I2=I3=...=In=Co x i
- Veamos un ejemplo de sistema de amortización americano:
La empresa Andalucía Vende compra una envasadora por un importe de 50.000€. Para realizar la adquisición solicita un préstamo a su entidad financiera con las siguientes condiciones de financiación:
- Duración del préstamo: 10 años.
- Interés de la operación: 12 % anual.
- Capital: 50.000 €.
- Sistema de amortización: americano (reembolso único de capital).
Los cálculos que debemos realizar quedan recogidos en la siguiente tabla:
Cálculo de la amortización de un préstamo. Sistema americano Operación Cálculo Cálculo de la cuota de interés periódica a pagar durante los 10 años que dura el préstamo. 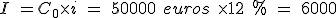
Esta es la cantidad que el prestatario deberá pagar en cada vencimiento en concepto de intereses.
Calculo de la anualidad del último vencimiento. 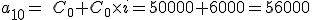
En el último periodo el prestatario deberá realizar el pago de la cuota correspondiente a los intereses más el reembolso del capital prestado.
Paralelamente se crea el llamado fondo de constitución o sinking fund que consiste en depositar una cantidad de dinero anualmente en una cuenta de ahorro a un interés determinado de forma que al finalizar esa imposición tengamos un montante igual al capital inicial del préstamo, pudiendo cancelarlo sin que le suponga a la empresa un gran esfuerzo.
- Veamos otro ejemplo con fondo de constitución:
En esta ocasión, Andalucía Vende pide un préstamo para la adquisición de un vehículo por valor de 30.000€. Las condiciones del préstamo son las siguientes:
- Interés efectivo anual: 4 %.
- Duración: 3 años.
- Se crea una cuenta de ahorro al 6 % de interés efectivo anual para constituir un fondo mediante cuotas constantes cuyo importe sea igual al capital concedido.
- Se pide, calcular la cuota de interés a pagar durante el periodo del préstamo y la anualidad o término amortizativo para constituir el fondo del importe del préstamo.
| Operación | Cálculo |
|---|---|
| Cálculo de la cuota de interés periódica a pagar durante los 3 años que dura el préstamo. |
Esta es la cantidad que el prestatario deberá pagar en cada periodo en concepto de intereses. |
| Calculamos la anualidad, que es el valor final de una renta pospagable, inmediata, constante y temporal. |
|
| Ingresará en la cuenta de ahorro un fondo anual de: | 9.423,29 €. |
4.3.- Amortización por el sistema francés.

Imagina que necesitas pedir un préstamo para adquirir una maquinaria y tras solicitar la información oportuna a tu entidad financiera, ésta te indica, entre otros aspectos, que el sistema de amortización que aplicarán a esta operación es el sistema francés ¿a que se refieren con esta información?
El sistema de amortización francés o, también llamado, de términos amortizativos constantes, se caracteriza porque:
- Los términos amortizativos permanecen constantes durante toda la vida del préstamo.
a1=a2=a3=...=an=a
- El tanto de amortización permanece constante durante toda la vida del préstamo.
i1=i2=i3=...=in=i
De lo anterior se desprende:
- Las anualidades son todas iguales.
- Los intereses de cada periodo van disminuyendo para cada anualidad.
- Las cuotas de amortización de cada periodo van aumentando.
La anualidad se obtiene planteando la siguiente equivalencia financiera:
![]()
![]()
Los términos amortizativos, anualidades, se descomponen en dos partes, cuota de amortización y cuota de interés:
![]()
En este sistema de amortización, al principio de la vida del préstamo la cuota de intereses es mayor, y la cuota de amortización es menor, progresivamente, con el paso del tiempo, esta tendencia se invierte, llegando al final de la vida del préstamo pagando una menor cuota de intereses y una mayor de amortización, pero siendo siempre igual la anualidad a pagar.
A continuación aprenderás a calcular la cuota de amortización en un periodo determinado (k):
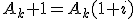
![]()
Por último, para calcular la deuda pendiente en un periodo determinado (k):
![]()
A continuación puedes practicar con un ejemplo de amortización de un préstamo. Se trata de un ejercicio en el que se presenta de forma clara y detallada todas las operaciones a seguir en la amortización de un préstamo.
4.4.- Préstamos con amortización fraccionada.

En los casos en los que la amortización de los préstamos se realiza en periodos inferiores al año, se aplicarán las mismas fórmulas que has estudiado en los apartados anteriores, pero deberás tener en cuenta algunas variaciones:
- El número de periodos será (n x m).
- La tasa de interés efectiva será la del subperido (im).
Es muy normal que te encuentres con tres tipos de tantos:
- El tanto efectivo anual (i) o TAE en el caso de no existir gastos ni comisiones.
- El tanto de efectivo fraccionado (im).
- El tanto nominal (in).
En estos casos, el valor de la anualidad será:
![]()
Veamos el siguiente ejemplo:
Luna está pensando en independizarse y solicita a su entidad financiera un préstamo hipotecario de 150.000€ para comprarse un apartamento. Las condiciones del préstamo consisten en pagar cuotas trimestrales durante 20 años al 3% de interés efectivo anual.
| Operación | Cálculo |
|---|---|
| Cálculo del tipo de interés equivalente. |
El interés de la operación es anual, pero las cuotas a pagar son trimestrales, por lo tanto tenemos que calcular el interés equivalente. Para ello: (1+0,03)=(1+i4 )^4→i4=0,007417 |
| Cálculo de la anualidad. |
Se trata de un préstamo a amortizar por el sistema francés. Para calcular el valor de la anualidad utilizaremos la fórmula que hemos aprendido:
Esta anualidad la pagará en cada trimestre, durante 80 trimestres (trimestres en 20 años). |
4.5.- Préstamos con tipos de interés variable.

Tienes que saber que lo habitual es que te encuentres en una situación en la que las entidades financieras te ofrezcan operaciones de préstamo (como por ejemplo los hipotecarios) a interés variable. Hasta ahora hemos realizado los cálculos teniendo en cuenta que los intereses eran fijos.
En este caso te surgirá la siguiente pregunta: ¿Cuál será el valor de la anualidad si tenemos que revisar periódicamente el tipo de interés en el préstamo? Para poder realizar el cálculo tienes dos opciones:
- En el momento que cambia el tipo de interés, también se deberá cambiar el valor de la anualidad, la cual se debe calcular en función del capital pendiente de amortizar que hay en el momento en el que se revisa el tipo de interés.
- Si queremos mantener el mimo valor de la anualidad, lo único que variará será el tiempo de la duración del préstamo, ya que partimos del mismo capital pendiente en ambos casos pero con un tipo de interés diferente.
Las entidades financieras revisan los tipos de interés aplicados de forma periódica (según lo acordado en el contrato), en ese momento, si hay variación, se ha de modificar el cuadro de amortización en base a las nuevas condiciones. Normalmente se toma como referencia para la variación de los tipos de interés el EURIBOR al cual se le aplica un porcentaje de incremento o diferencial que estará en función al grado de vinculación que se tenga con la entidad financiera, además del número de productos que se contrate con ella, como por ejemplo, seguros, planes de pensiones, etc.
A continuación puedes practicar con un ejemplo de amortización de un préstamo a interés variable. Se trata de un ejercicio en el que se presenta de forma clara y detallada todas las operaciones a seguir en la amortización de un préstamo, pero con la peculiaridad de que en este caso, a diferencia del anterior ejemplo, nos encontramos un préstamo a interés variable.
5.- Análisis de las operaciones de arrendamiento financiero.

Carlos se reúne con Luna para comentarle que su próximo reto será el estudio de las operaciones de leasing. Carlos le explica que gracias a las operaciones de leasing, la empresa Andalucía Vende puede disponer de maquinaria sin necesidad de realizar grandes desembolsos, por lo que se trata de un medio muy válido y útil de financiación para las empresas, sobretodo para las pequeñas y medinas empresas.
Luna se encuentra expectante ante este nuevo reto.
En unidades anteriores has estudiado qué es y en qué consisten las operaciones de leasing. Ahora es el momento de que afrontes el estudio financiero de estas operaciones.
Las empresas utilizan el arrendamiento financiero como medio de financiación, ya que gracias a él pueden acceder a determinados bienes (como por ejemplo maquinarias) que de no ser por este tipo de operaciones, les resultaría realmente difícil poder disponer de tales bienes, debido, principalmente, a las grandes cantidades de recursos que necesitarían. Se trata por lo tanto de una forma de disponer de bienes necesarios para el desarrollo de la actividad de la empresa sin necesidad de desembolsar grandes cantidades de recursos económicos.
El arrendamiento financiero es un medio muy utilizado por las pequeñas y medianas empresas, ya que son éstas las que presentan una mayor dificultad de acceso al crédito.
En el ámbito financiero se llega a decir que si el arrendamiento financiero no existiera, seguro que habría que inventarlo, ya que la facilidad, sencillez y economía que ofrece a las empresas para la adquisición, renovación, mantenimiento, control y gestión de sus bienes de equipo le hace ser una herramienta fundamental de la empresa actual.
A continuación vas a aprender un poquito más sobre este tipo de operaciones.
5.1.- El leasing.

En unidades anteriores has estudiado en qué consiste el leasing (tanto financiero como operativo) así como las ventajas y desventajas que implica este tipo de operaciones financieras. Ahora es el momento de afrontar el procedimiento de su cálculo.
Recordarás que en este tipo de operaciones, cuando finaliza el periodo de arrendamiento, el arrendatario tiene varias opciones:
- Adquirir el bien pagando lo que se denomina valor residual.
- Rescindir el contrato y devolver el bien objeto de leasing a la empresa de arrendamiento financiero.
- Volver a negociar un nuevo contrato de leasing sobre el mismo bien o uno nuevo pagando nuevas cuotas.
El cálculo de las operaciones de arrendamiento financiero se igual que el realizado en las operaciones de préstamo con la diferencia de lo que hemos denominado como valor residual. Deberemos conocer cuál es el valor residual de la operación o, en caso de desconocerlo, calcularlo.
En las operaciones de leasing, te puedes encontrar con cuotas de alquiler prepagables, pospagables, con interés vencido o con interés anticipado, si bien es cierto que en la realidad, lo más habitual son los pagos prepagables y con interés anticipado, para que de esa forma, la última cuota de amortización coincida con el valor residual.
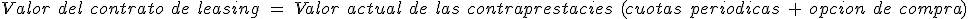
vc=a x an-1i
![]()
El tipo de interés utilizado es un tanto efectivo anual, por lo tanto, en caso de contratar unos pagos de periodicidad inferior al año (meses, trimestres, semestres, etc.), deberemos utilizar el interés equivalente (im).
Puede ocurrir que el valor de la opción de compra no coincida con el valor del resto de pagos periódicos, en este caso, el valor del contrato de leasing se calculará de la siguiente forma:
![]()
![]()
Veamos el siguiente ejemplo:
Se quiere calcular la anualidad del arrendamiento de un vehículo industrial cuyo valor es de 13.000€ con un valor residual de 3.000€, a alquilar durante 5 años. Si al principio de cada año se paga a un interés anticipado del 3,5% anual.
| Operación | Cálculo |
|---|---|
| Cálculo del tipo de interés equivalente. | |
| Cálculo de la anualidad. |
Recuerda que:
|
| Cantidad a pagar. | 2.570,77 € (sin IVA), para calcular la cantidad con IVA, la multiplicaremos por 1,18 obteniendo un resultado de 3.033,51 €. |
5.2.- Aplicación financiera de la hoja de cálculo.

A lo largo de tu vida profesional y personal tendrás que utilizar muy asiduamente las nuevas tecnologías. Estas tecnologías han sido creadas para hacerte más fácil tú día a día. Si nos centramos en el ámbito profesional, la utilización de las nuevas tecnologías te ha de facilitar el desempeño de tú trabajo, contribuyendo a aumentar tu eficiencia. Un claro ejemplo de estas herramientas tecnológicas son las hojas de cálculo, a través de las cuales puedes realizar cálculos complejos de una manera sencilla disminuyendo el tiempo empleado en dichas operaciones de cálculo.
A través del siguiente vídeo puedes acceder a un vídeo en el que se explica detalladamente cómo realizar un cuadro de amortización de un leasing mediante una hoja de cálculo.
En esta presentación flash sobre el esquema del leasing. En esta presentación podrás ir viendo como se forma el circuito de leasing con el paso de cada una de las diapositivas.
6.- Análisis de las operaciones de empréstitos.
Luna se encuentra ante la última parte de esta fase de su formación. Es hora de conocer la importancia de los empréstitos como fuente de financiación para las empresas.
Carmen quiere reunirse con Luna para tratar personalmente este tema, ya que para ella se trata de un tema delicado y quiere supervisar personalmente su formación. Le realizará una introducción a este tema, pero no profundizará mucho, sobre todo por su complejidad. Para Carmen es importante porque gracias a los empréstitos las empresas pueden obtener grandes cantidades de recursos económicos, pero a la vez tienen un tratamiento algo complicado.
Luna acepta el reto aunque está un poco nerviosa al tener a Carmen como tutora de esta parte de formación, pero el trato de Carmen es muy cercano y hace que Luna se sienta muy bien. Realmente Luna está sintiéndose cada vez más integrada y su ilusión sería poder quedarse en la empresa, aunque sabe que es complicado, sobretodo por la situación de crisis que actualmente estamos sufriendo, pero su entusiasmo no decae y está dispuesta a dar lo máximo.


Como has visto en unidades anteriores, las empresas (y también los organismos públicos) necesitan de recursos financieros para poder desarrollar sus proyectos de inversión, y son varias las opciones que tienen para acceder a esa financiación. El empréstito es una de esas modalidades de financiación que permite obtener recursos sin necesidad de acudir a una entidad financiera.
El empréstito consiste en dividir la cantidad que se necesita (préstamo) en un gran número de pequeñas partes iguales (participaciones), que coloca entre multitud de inversores. Estas partes del empréstito vienen representadas por títulos valores. Todos los títulos valores correspondientes a una misma emisión presentan las mismas características: importe, tipo, vencimiento, etc.
La entidad que emite los títulos se denomina emisor, que como he comentado anteriormente, puede ser tanto una empresa privada como un ente público. El inversor que suscribe los títulos valores se denomina "obligacionista".
Los títulos-valores ofrecen al inversor los siguientes derechos:
- Recibir periódicamente intereses por los fondos prestados.
- Recuperar los fondos prestados al vencimiento del empréstito.
Los empréstitos pueden ser clasificados de diferentes formas:
| Criterios | Clases de empréstitos |
|---|---|
| Según el emisor. | Se diferencian entre deuda pública (emitida por entidades públicas) y deuda privada (emitida por entidades privadas). |
| Según el vencimiento. | Se distinguen entre deuda amortizable (cuando tienen un vencimiento), deuda perpetua (no tienen vencimiento, aunque el emisor se guarda el derecho a poder amortizarla cuando lo considere oportuno). Hay que tener mucho cuidado con la deuda perpetua, ya que te puede traer bastantes problemas, sobretodo si no entendemos bien lo que nos están ofreciendo. |
| Según la modalidad de amortización. | Se distinguen entre empréstitos con vencimiento periódicos parciales, donde en cada periodo se amortiza un número determinado de títulos o una parte de todos los títulos, y los empréstitos de una amortización al vencimiento, donde solo se producirá la amortización de los títulos al finalizar la operación. |
| Según el valor de emisión. | Se distinguen entre títulos emitidos a la par (se emiten por su valor nominal), emitidos bajo la par (se emiten a un precio inferior a su valor nominal) y emitidos sobre la par (se emiten a un precio superior a su valor nominal). |
| Según el pago de intereses. | Se distinguen empréstitos con pagos de intereses periódicos o empréstitos de cupón cero donde solo existe un único pago de intereses en la fecha de vencimiento del empréstito. |
6.1.- Los empréstitos.

Luna está aprendiendo que los empréstitos surgen de la necesidad financiera o de recursos de la empresa. En ocasiones, las empresas necesitan de grandes cantidades de recursos económicos para poder hacer frente a costosas inversiones, para lo cual, la empresas no pueden acceder a un único préstamo, sino que son necesario un conjunto de ellos. Es en estos casos cuando las empresas pueden recurrir a una emisión de empréstitos.
El importe de una obligación se denomina valor nominal y da derecho al obligacionista (propietario de la obligación) al cobro de un interés anual o semestral (cupón) y a la devolución del valor de la obligación (amortización de la obligación) conforme a las condiciones establecidas.
| Significado de los acrónimos | Acrónimos. |
|---|---|
| Valor nominal del empréstito. | C0=C x N. |
| Número de títulos emitidos. | N. |
| Valor nominal del título. | C. |
| Valor de emisión del empréstito. | E. |
| Emisión a la par. | E=C. |
| Valor de emisión bajo la par. | E<C. |
| Prima de emisión. | Pe=C - E. |
| Valor de reembolso o amortización de una obligación. | Ck. |
| Emisión sobre la par. | Ck>C. |
| Prima de amortización. | Pk=Ck - C. |
| Número de obligaciones amortizadas. | Mk. |
| Duración de un empréstito. | n. |
| Intereses satisfechos. | lk. |
| Cupón anual. | C x i. |
| Anualidad. | a. |
| Valor del lote. | Lk. |
Veamos el siguiente ejemplo:
La empresa Andalucía Vente emite un empréstito de 10.000.000 € con las siguientes condiciones:
- El valor nominal de una obligación es de 100 €, durante 10 años a un interés efectivo semestral del 3 %.
- El valor de suscripción de una obligación es de 99 € y su valor de reembolso es del 110 %.
Con los anteriores datos, las variables del empréstito serán:
n (tiempo) = 10 años.
C (valor de la obligación) = 100 €.
E (Valor de emisión de la obligación) = 99 €.
Pe(prima de emisión)=C - E=100 € - 99 €= 1 €
C x i2(cupón anual)= 100 € x 0,03= 3 € de cupón por obligación.
C0 (valor nominal del empréstito)=C x N → 10.000.000 €=100 € x N→N=100.000 obligaciones.
Ck(valor de reembolso)= 100 € x 1,10=110 € valor de reembolso por obligación.
Pk(prima de amortización)= Ck - C=110 € - 100 €=10 € de prima de reembolso o amortización.
Anexo I.- Liquidación de una cuenta de crédito.
Análisis de las operaciones de líneas de créditos.
A continuación vas a practicar con un caso práctico de una póliza de crédito.
La empresa Andalucía Vende ha contratado con su entidad financiera una póliza de crédito con las siguientes condiciones:
- Límite de crédito: 30.000 €.
- Interés deudor: 15 %.
- Interés excedido: 25 %.
- Interés acreedor: 3 %.
- Comisión por disponibilidad: 0,5 % trimestral.
- Comisión por excedido: 0,1 % trimestral.
- La liquidación se realizará por trimestres vencidos.
A lo largo del primer periodo de liquidación se han producido los siguientes movimientos:
- 15-04 Concesión de la póliza. Cargo de 500 €. por comisiones.
- 20-04 Pago de una factura de 7.000 €.
- 10-05 Pago de un talón de 15.000 €.
- 15-06 Pago de una factura de 3.000 €.
A lo largo del segundo periodo de liquidación se han producido los siguientes movimientos:
- 18-07 Pago de facturas por valor de 5.000 €.
- 25-09 Ingreso en efectivo de 32.000 €.
A continuación se realizarán las liquidaciones de los periodos comprendidos entre el 15 de Abril y el 15 de Julio, y del 15 de Julio al 15 de Octubre.
- Comenzaremos por la liquidación del primer periodo comprendido entre el 15 de Abril y el 15 de Julio:
Cuadro de liquidación de una póliza de crédito Fecha Concepto Cuantía Signo Saldo Signo Días Números deudores Números excedidos Números acreedores 15-04. Comisión de apertura. 500 €. D 500€. D 5 2.500 20-04. Pago factura. 7.000 €. D 7.500€. D 20 150.000 10-05. Pago talón. 15.000 €. D 22.500€. D 36 810.000 15-06. Pago facturas. 3.000 €. D 25.500€. D 30 765.000 15-07. 91 1.727.500 - Cálculo de los números comerciales deudores:
Para realizar éste cálculo nos basaremos en la siguiente fórmula:
A continuación realizamos los cálculos:
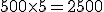
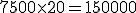
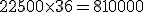
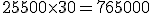
- A continuación calcularemos los intereses deudores:
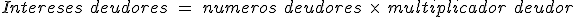
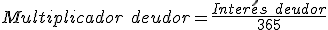
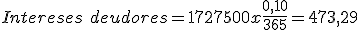
- A continuación calcularemos la comisión de disponibilidad:
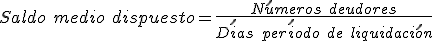

Cuadro para el cálculo del saldo después de la liquidación Conceptos Cálculos Resultados Saldo medio no dispuesto. 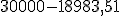
11.016,49 €. Comisión por disponibilidad. 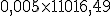
55,08 €. Saldo después de la liquidación. 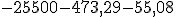
-26.028,37 € (deudor). - Cálculo de los números comerciales deudores:
- Seguidamente realizaremos los cálculos del siguiente periodo de liquidación, que corresponderá al periodo comprendido entre el 15 de Julio y el 15 de Octubre.
Tenemos que comenzar realizando la liquidación con los datos del anterior periodo, en la columna cuantía se incluirán las comisiones (55,08 €.) y los intereses (473,29 €.) que da un total de 528,37 €. El saldo del que partiremos será el total del saldo después de la liquidación calculado en el apartado anterior, es decir, 26.028,37 €.
Cuadro de liquidación de una póliza de crédito Fecha Concepto Cuantía Signo Saldo Signo Días Números deudores Números excedidos Números acreedores 15-07. Liquidación anterior. 528,37 €. D. 26.028,37 €. 3 78.085,11. 18-07. Pago factura. 5.000 €. D 31.028,37 €. D. 69. 2.070.000. 70.957,53. 25-09. Ingreso. 32.000 €. H. 971,63 €. H. 20. 19.432,6. 15-10. 92. 2.148.085,11. 70.957,53. 19.432,6. En esta ocasión nos encontramos con un excedido el 18 de Julio ya que el saldo de la cuenta es superior al límite establecido en la póliza de crédito de 30.000 €. Igualmente nos encontramos con un saldo acreedor de 377,13 € durante un periodo de 20 días. A continuación realizaremos los cálculos:
- Cálculo de los números comerciales deudores:
Para realizar éste cálculo nos basaremos en la siguiente fórmula: Saldo x días.
A continuación realizamos los cálculos:
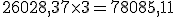
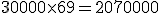
Total: 2.148.085,11
- Cálculo de los números excedidos:
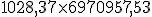
- Cálculo de los números acreedores:
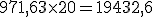
- A continuación calcularemos los intereses:
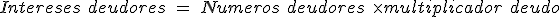
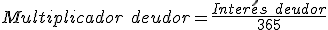
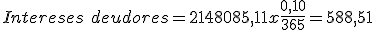
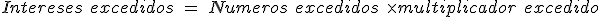
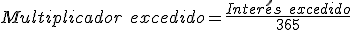
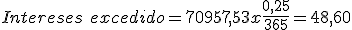
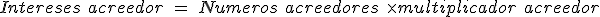
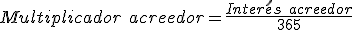
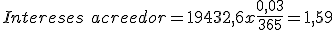
- A continuación calcularemos la comisión de disponibilidad:
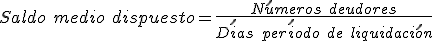
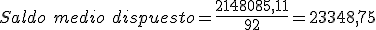
Cuadro para el cálculo del saldo después de la liquidación Conceptos Cálculos Resultados Saldo medio no dispuesto. 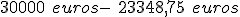
6.651,24 €. Comisión por disponibilidad. 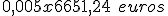
33,25 €. Comisión por excedido. 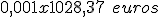
1,02 €. Saldo después de la liquidación. 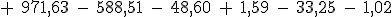
-301,84 € (acreedor). - Cálculo de los números comerciales deudores:
Anexo II.- Liquidación de una cuenta corriente (I).
Análisis de las operaciones con cuentas corrientes.
A continuación vas a practicar con un caso práctico de cuenta corriente.
La empresa Andalucía Vende tiene contratada una cuenta corriente con su entidad financiera Banco General con las siguientes condiciones:
- Tipo de interés anual para saldos acreedores: 2 %.
- Tipo de interés anual para descubiertos: 18 %.
- Comisión sobre mayor saldo descubierto: 3 % sobre el mayor saldo descubierto contable en el periodo de liquidación.
- Fecha de liquidación: 30 de Abril.
- La entidad bancaria utiliza 365 para calcular los intereses deudores y acreedores.
- El IRC es del 19 %.
A lo largo del primer periodo de liquidación se han producido los siguientes movimientos:
- 01-03 Apertura, cuyo vencimiento es el 1 de Marzo.
- 14-03 Ingreso en efectivo: 1.000 €, cuyo vencimiento es el 15 de Marzo.
- 14-03 Letra a su cargo: 300 €, cuyo vencimiento es el 5 de Marzo.
- 27-03 Transferencia a su favor: 500 €, cuyo vencimiento es el 28 de Marzo.
- 30-03 Pago del recibo de teléfono: 200 €, cuyo vencimiento es el 3 de Abril.
- 10-04 Entrega en efectivo: 2.000 €, cuyo vencimiento es el 11 de Abril.
A continuación se realizarán las liquidaciones del periodo comprendido entre el 01 de Marzo y el 30 de Abril:
| Fecha | Fecha valor | Concepto | Debe | Haber | Saldo | Signo | Días | Números deudores | Números acreedores |
|---|---|---|---|---|---|---|---|---|---|
| 14-03 | 5-03 | Letra a su cargo. | 300 € | 300 € | D | 10 | |||
| 14-03 | 15-03 | Ingreso en efectivo. | 1.000 € | 700 € | H | 13 | 9.100 (2) | ||
| 27-03 | 28-03 | Transferencia a su favor. | 500 € | 1.200 € | H | 6 | 7.200 (3) | ||
| 30-03 | 03-04 | Pago recibo de teléfono. | 200 € | 1.000 € | H | 8 | 8.000 (4) | ||
| 10-04 | 11-04 | Entrega en efectivo | 2.000 € | 3.000 € | H | 19 | 57.000 (5) | ||
| 30-04 | 56 |
El saldo antes de la liquidación es de 3.000 €.
- Cálculo de los números comerciales acreedores:
Para realizar el cálculo de los saldos acreedores debemos realizar la siguiente multiplicación:
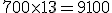
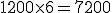
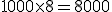
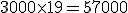
Total: 81.300
- A continuación calcularemos los intereses acreedores:
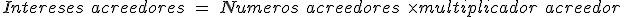
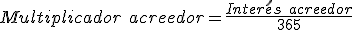
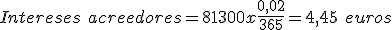
- Cálculo de los números comerciales deudores:
Para realizar el cálculo de los saldos acreedores debemos realizar la siguiente multiplicación:
Saldo x número de días
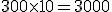
Total: 3.000
- A continuación calcularemos los intereses deudores:
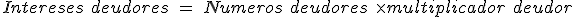
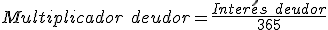
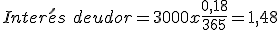
- A continuación calcularemos la retención sobre los intereses acreedores:
4,45€x19%=0,85€
- A continuación se calcula la comisión sobre mayor descubierto.
En este caso la operación se ha de realizar sobre la fecha de la operación, no sobre la fecha valor. Por lo tanto, para ver si procede ésta habrá que ordenar los movimientos según se han producido realmente (fecha de la operación):
| Fecha | Fecha valor | Concepto | Debe | Haber | Saldo | Signo | Días |
|---|---|---|---|---|---|---|---|
| 14-03. | 5-03. | Letra a su cargo. | 300 €. | 300 €. | D. | 0. | |
| 14-03. | 15-03. | Ingreso en efectivo. | 1.000 €. | 700 €. | H. | 13. | |
| 27-03. | 28-03. | Transferencia a su favor. | 500 €. | 1.200 €. | H. | 6. | |
| 30-03. | 03-04. | Pago recibo de teléfono. | 200 €. | 1.000 €. | H. | 8. | |
| 10-04. | 11-04. | Entrega en efectivo. | 2.000€. | 3.000 €. | H. | 19. | |
| 30-04. | 46. |
En este ejemplo no se han producido descubiertos, ya que el 14 de Marzo la cuenta está en descubierto por una operación en la que se han cargado 300 € por el pago de una letra, pero el mismo día, Andalucía Vende realiza un ingreso en la cuenta por 1.000 €, por lo que pasa a "estar en positivo".
El saldo después de la liquidación quedará de la siguiente forma:
+ saldo + intereses acreedores - intereses deudores - retención - comisión por descubierto(3000 € + 4,45 €- 1,48 € - 0,85 € - 0=3002,12 €).
Anexo III.- Liquidación de una cuenta corriente (II).
Análisis de las operaciones con cuentas corrientes.
A continuación vas a practicar con otro caso práctico de cuenta corriente.
La empresa Cuadrados S.L tiene contratada una cuenta corriente con su entidad financiera Banco Generoso con las siguientes condiciones:
- Tipo de interés anual para saldos acreedores: 5 %.
- Tipo de interés anual para descubiertos: 10 %.
- Comisión de mantenimiento: 3 €.
- Fecha de liquidación: 31 de Marzo.
- La entidad bancaria utiliza 360 para calcular los intereses deudores y acreedores.
- El IRC es del 19 %.
A lo largo del primer periodo de liquidación se han producido los siguientes movimientos:
- 01-03 se dispone de un saldo a favor de 40.000 €.
- 04-03 Ingreso de un cheque: 1.500 €. La facha valor: 05-03
- 05-03 Pago de impuestos: 2.000 €.
- 10-03 Pago de recibo de teléfono: 350 €.
- 14-03 Pago a un proveedor: 50.000 €.
- 20-04 Transferencia a favor de la empresa: 25.000 €. La fecha valor: 21-03
A continuación se realizarán las liquidaciones del periodo comprendido entre el 01 de Marzo y el 31 de Marzo:
| Fecha | Fecha valor | Concepto | Debe | Haber | Saldo | Signo | Días | Números deudores | Números acreedores |
|---|---|---|---|---|---|---|---|---|---|
| 01-03. | 01-03. | Saldo. | 40.000. | 40.000. | H. | 4. | 160.000 (1). | ||
| 04-03. | 05-03. | Ingreso cheque. | 1.500. | 41.500. | H. | 0. | |||
| 05-03. | 05-03. | Paga impuestos. | 2.000. | 39.500. | H. | 5. | 197.500 (2). | ||
| 10-03. | 10-03. | Pago teléfono. | 350. | 39.150. | H. | 4. | 156.600 (3). | ||
| 14-03. | 14-03. | Pago a proveedor. | 50.000. | 10.850. | D. | 7. | 75.950 (4). | ||
| 20-03. | 21-03. | Ingreso (transferencia). | 25.000. | 14.150. | H. | 10. | 141.500 (5). | ||
| 31-03. | . | 655.600 . |
El saldo antes de la liquidación es de 14.150 €.
- Cálculo de los números comerciales acreedores:
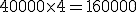
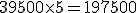
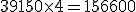
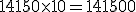
Total: 655.600
- A continuación calcularemos los intereses acreedores:
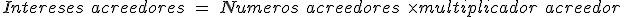
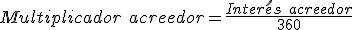
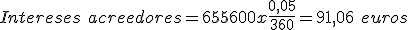
- Cálculo de los números comerciales deudores:
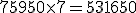
Total: 531.650
- A continuación calcularemos los intereses deudores:
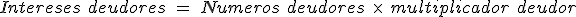
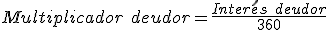
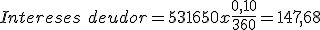
- A continuación calcularemos la retención sobre los intereses acreedores:
91,06 € x 19 %=17,30 €.
En este ejemplo si se han producido descubiertos, ya que el 14 de Marzo la cuenta está en descubierto por una operación en la que se han cargado 50.000€ por el pago a un proveedor.
El saldo después de la liquidación quedará de la siguiente forma:
+ saldo + intereses acreedores - intereses deudores - retención - comisiones (14150 € + 91,06 € - 177,68 € - 17,30 € - 3=14043,08 €).
Anexo IV.- Amortización de un préstamo.
La empresa Andalucía Vende solicita a su entidad financiera un préstamo con el fin de comprar un vehículo comercial por valor de 50.000 €. Las condiciones son las siguientes:
- Plazo del préstamo: 3 años.
- Tasa de interés efectivo anual: 10 %.
- Sistema de amortización francés.
Lo primero que tienes que realizar es el cálculo del valor de la anualidad o término amortizativo:
![]()
![]()
![]()
En este caso, Andalucía Vende deberá pagar una anualidad de 20.106,16 €.
A continuación construiremos el cuadro de amortización:
| Años |
Anualidad. (a) |
Cuota de interés. (Is) |
Cuota de amortización.
(As) |
Amortización acumulada Mn=M(n-1)+An |
Capital pendiente Cn=C(n-1)-An |
|---|---|---|---|---|---|
| 0 |
50.000 C0=50000 |
||||
| 1 | 20.106,16 |
5.000 I1=C0 x i |
15.106,16 A1=a - I1 |
15.106,16 M1=M0 + A1 |
34.893,84 C1=C0 - A1 |
| 2 | 20.106,16 |
3.489,84 I2=C1 x i |
16.616,32 A2=a - I2 |
31.722,48 M2=M1 + A2 |
18.277,52 C2=C1 - A2 |
| 3 | 20.106,16 |
1.827,75 I3=C2 x i |
18.278,41 A3=a - I3 |
50.000 M3=M2 + A3 |
-0,89 C3=C2 - A3 |
En la última celda de la columna de capital pendiente aparece una cantidad negativa de 0,89. Debería ser cero, pero por el redondeo de los decimales ha provocado ese pequeño desajuste.
Imagina ahora que queremos conocer la cuota de amortización en un periodo determinado, por ejemplo en el año 2, sin necesidad de tener que realizar el cuadro de amortización. En este caso debemos recurrir a la siguiente fórmula:
![]()
Antes deberemos calcular la cuota de amortización para el periodo uno:
![]()
La cuota de amortización para el periodo dos será:
![]()
Recuerda que no cuadra exactamente debido al redondeo con los decimales.
Ahora vamos a calcular la deuda pendiente para un periodo determinado, por ejemplo para el dos, sin necesidad de tener que realizar el cuadro de amortización. Para ello debemos emplear la siguiente fórmula:
![]()
Aplicando la fórmula tendremos:
![]()
Recuerda que el resultado no es exacto a causa del redondeo con los decimales.
Anexo V.- Amortización de un préstamo a interés variable.
La empresa Andalucía Vende solicita a su entidad financiera un préstamo hipotecario con el fin de comprar un edificio para destinarlo a oficinas por valor de 300.000€. Las condiciones son las siguientes:
- Plazo del préstamo: 20 años.
- Tasa de interés efectivo anual: 2,5 % revisable anualmente al EURIBOR más un diferencial del 0,25% (se trata de un bajo porcentaje debido al alto grado de vinculación con la entidad financiera).
- Vamos a tener en cuenta que las anualidades se pagan por años, por lo que operaremos con el tipo de interés efectivo anual. En el caso de realizarse el pago de las anualidades de forma mensual, deberíamos calcular el tipo de interés equivalente mensual y operar por meses, tal y como se muestra en el ejemplo del punto cuatro de la cuarta parte de la unidad.
- El valor de la anualidad del primer año.
- El capital pendiente a principios del segundo año.
- El valor de la nueva anualidad para el segundo año teniendo en cuenta que el EURIBOR ha sido del 2,75 %.
- El nuevo periodo de duración del préstamo si se decide pagar la misma anualidad.
- Lo primero que tienes que vamos a realizar es calcular la anualidad del pago del primer año:
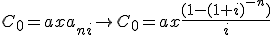
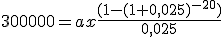
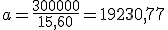
- Ahora calcularemos el capital pendiente a principios del segundo año:
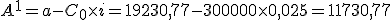
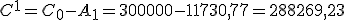
Cálculo de la amortización de un préstamo. Sistema francés Años Anualidad
(a).
Cuota de interés
(Is)
Cuota de amortización
(As)
Amortización acumulada
Mn=M(n-1)+An
Capital pendiente
Cn=C(n-1)-An
0 300.000
C0=300000
1 19.230,77 7.500
I1=C0 x i
11.730,77
A1=a - I1
11.730,77
M1=M0 + A1
288.269,23
C1=C0 - A1
- El valor de la nueva anualidad en caso de revisar el tipo de interés:
En este caso la nueva tasa de interés que se deberá aplicar será del EURIBOR más el diferencial contratado que es del 0,25. Por lo tanto:
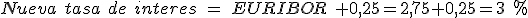
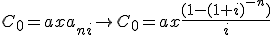
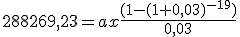
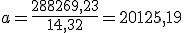
Esta es la anualidad que pagará durante el segundo año.
- El nuevo periodo en caso de querer mantener la misma anualidad:
Nos encontramos en el comiendo del segundo año y nuestra entidad financiera nos ha revisado al alza el tipo de interés (ha pasado a un 3% tal y como acabas de calcular), pero queremos seguir pagando la misma anualidad que pagábamos el primer año. Esta decisión afectará a la duración del préstamo, pero ¿Cuánto exactamente?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Este momento quedaban 19 años para finalizar el préstamo (recuerda que estábamos al comienzo del segundo año) pero desde este momento, y manteniendo las anualidades del primer año, deberemos prolongar el plazo a 20 años y dos meses, es decir, un año más de lo que iba a durar la operación en un principio.
A continuación vamos a calcular la TAE partiendo de los datos anteriores, e incluiremos los nuevos gastos y comisiones por la apertura del mismo. Los datos son los siguientes:
- Importe del préstamo: 300.000 €.
- Duración: 20 años.
- Interés efectivo anual: 2,5 %.
- Anualidad: 19.230,77 €.
- Comisión de apertura: 1 %.
- Gastos de tasación: 0,5 %.
- Seguro de vida obligatorio: 300 €.
- Gastos de notaría: 500 €. (los gastos de notaría no se incluyen en el cálculo de la TAE según la Circular 8/90 del Banco de España).
- Calcular el importe de la prestación sin gastos:
Valor del préstamo: 300.000 €.
Comisión de apertura: 300000 x 0,01=3000 €
Gastos de estudio: 300000 x 0,05=1500 €
Seguro de Vida: 300 €.
300000 - 3000 - 1500 - 300=295200 €
- Partiendo del nuevo valor del préstamo, calculamos la TAE, teniendo en cuenta el valor de la anualidad obtenida:
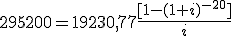
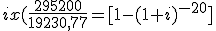
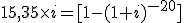
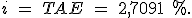
A través a la web del Banco de España vas a poder realizar una simulación del cálculo de la TAE que te permitirá calcular el importe de los intereses brutos a percibir en un depósito bancario, con un Tipo de Interés, plazo y periodicidad de pago determinados, calculando además su Tasa Anual Equivalente.
Anexo.- Licencia de recursos.
| Recurso (1) | Datos del recurso (1) | Recurso (2) | Datos del recurso (2) |
|---|---|---|---|
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. EP006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. EP006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. EP006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. EP006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. EP006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD109. |
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. ECD006. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
 |
Autoría: Ministerio. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Ministerio. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. ECD001. |
 |
Autoría: Photodisc. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. V07. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD109. |
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. Comentarios para Unificación pasar a html Comentarios para Integración: Título: Préstamo variable Descripción: Documento que muestra el procedimiento sobre el cálculo de la amortización de un préstamo a interés variable. Nombre: GF03_CONT_R29_prestamovariable.pdf Autoría: Crístobal Castillo Morales. Licencia: Uso educativo no comercial. Procedencia: Elaboración propia. |
 |
Autoría: Ministerio de Educación. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: Fotograma extraído del video disponible en la dirección http://www.youtube.com/watch?v=KXR6dCR9wgY |
 |
Autoría: Photodisc. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. V07. |
 |
Autoría: Photodisc. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. V07. |
 |
Autoría: Stockbyte. Licencia: Uso Educativo no comercial para plataformas FpaD. Procedencia: CD-DVD Num. CD165. |
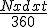 =
=