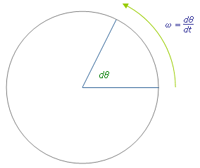
Este movimiento es muy habitual en nuestro entorno, piensa, por ejemplo, en la rueda de un vehículo, un motor, las manecillas de un reloj, una piedra atada con una cuerda, una ruleta ideal...
Todos realizan un movimiento circular uniforme. Es decir, un movimiento alrededor de un centro fijo y con una velocidad angular, ω, constante y, por lo tanto, una aceleración angular nula. La trayectoria del movimiento que describen es una circunferencia. Puesto que la velocidad angular es constante, se puede considerar que durante un tiempo t, medido en segundos, recorren un ángulo θ, medido en radianes. Y tenemos que la velocidad angular es el ángulo recorrido por unidad de tiempo, si hacemos que el tiempo sea infinitesimal el ángulo recorrido también lo será.
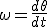 (1.1)
(1.1)
Integrando se llega a que el ángulo recorrido por un objeto que tiene un movimiento circular uniforme es una función del tiempo:
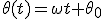 (1.2)
(1.2)
La ecuación (1.2) nos indica la posición del objeto en función del tiempo, donde θ0 es la posición que ocupa el cuerpo al inicio del tiempo, cuando t = 0.
De la propia definición de movimiento circular uniforme sabemos que es un movimiento periódico, entonces cuando pase un periodo de tiempo, T, el objeto ocupará la misma posición:
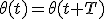 (1.3)
(1.3)
Durante este periodo el objeto ha recorrido un ángulo de 2π radianes, es decir, ha descrito una vuelta completa, con una velocidad angular constante, por lo que podemos calcular el periodo como:
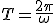 (1.4)
(1.4)
¿Cuántas vueltas dará el objeto por unidad de tiempo? A esta pregunta se puede responder fácilmente calculando la inversa del periodo, a esta nueva variable se la denomina frecuencia, ν, cuyas unidades son inverso de tiempo, el hertzio:
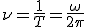 (1.5)
(1.5)
Ahora, vamos a proyectar la posición del cuerpo a lo largo de la trayectoria circular sobre el diámetro vertical, eje Y de la circunferencia. Observaremos que la proyección se mueve arriba y abajo, pasando por el centro de la circunferencia. Cuando el cuerpo ha realizado una vuelta completa, a lo largo de la trayectoria circular, la proyección sobre el diámetro ha recorrido dos veces el diámetro. El movimiento de la proyección a lo largo del diámetro también es un movimiento periódico puesto que el cuerpo que lo genera tiene un movimiento periódico.
Fácilmente se puede llegar a deducir la ecuación del movimiento de la proyección. Sabemos que esta proyección no es más que el seno del ángulo que forme la línea que une el centro de la circunferencia con el cuerpo. Y, puesto que el movimiento circular tiene una velocidad constante, sabemos que cuando han pasado t segundos el cuerpo se habrá desplazado un ángulo ωt, al que habrá que sumar el ángulo que formase antes de empezar el movimiento, φ. La distancia máxima que se separará la proyección del centro de la circunferencia, que tomaremos como origen del movimiento será la amplitud, por lo que podemos escribir la siguiente ecuación:
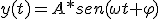 (1.6)
(1.6)
Es decir, la proyección realiza un movimiento armónico simple a lo largo del diámetro de la circunferencia del movimiento circular uniforme.
Número de radianes por unidad de tiempo.
En el caso del tiempo es el transcurso de una fracción infinitamente pequeña del mismo. En el caso del recorrido es un ángulo infinitamente pequeño.