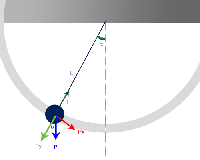
Un péndulo es una masa, m, que cuelga de un punto fijo gracias a un hilo inextensible y sin masa de longitud l. La masa se encuentra en reposo cuando el hilo se mantiene en posición vertical.
Ahora vamos a separar la masa de la posición de equilibrio haciendo que el hilo forme un ángulo θ con la vertical. Sobre la masa actúan las siguientes fuerzas:
- La tensión de la cuerda.
- El peso debido a la atracción gravitacional de la masa. Este se puede descomponer en sus dos componentes:
- Componente radial, de igual magnitud que la tensión de la cuerda y opuesto a esta.
- Componente tangencial, es el causante del movimiento de la masa para volver a su posición de reposo, que se puede calcular mediante:
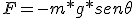 (1.7)
(1.7)
El signo negativo indica que la fuerza generadora del movimiento es opuesta a la elongación.
Cuando se suelta la masa esta vuelve a su posición de equilibrio, pero la velocidad alcanzada durante la trayectoria provoca que se pase de este punto y recorra un ángulo igual pero en sentido contrario, cuando la energía cinética se acaba vuelve a empezar.
En la ecuación 1.7 sustituimos el seno por su definición, y aplicamos la segunda ley de Newton:
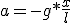 (1.8)
(1.8)
donde x es la distancia del cuerpo a la vertical. En la ecuación 1.8 sustituimos la aceleración por su definición y llegamos a la ecuación del péndulo simple que nos permite calcular la distancia del cuerpo respecto a la vertical en función del tiempo:
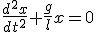 (1.9)
(1.9)
Una solución de esta ecuación 1.9 es la ecuación del movimiento armónico simple:
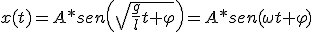 (1.10)
(1.10)
donde:
- A, es la amplitud, distancia máxima del cuerpo a la vertical.
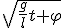 ,es la fase del movimiento en el instante t.
,es la fase del movimiento en el instante t.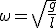 , es la frecuencia angular.
, es la frecuencia angular.- φ, es la fase inicial, la fase en t = 0, la posición del móvil antes de empezar el movimiento.
Distancia que separa el cuerpo de su posición de reposo, cuando realiza un movimiento armónico simple.
Energía debida al movimiento del cuerpo. Trabajo para que el cuerpo adquiera una cierta velocidad desde el reposo.
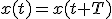 (1.11)
(1.11)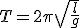 (1.12)
(1.12)