1.1.3 Muelle

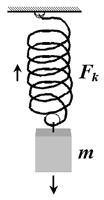
En este caso, un cuerpo de masa m está unido a un punto fijo en el techo o plano superior mediante un muelle. Para facilitar los cálculos vamos a suponer que el muelle no tiene masa y que cumple la ley de Hooke. Esta ley indica que cuando separo el cuerpo de su posición de equilibrio, aparece una fuerza elástica, que se opone a ese desplazamiento y que trata de llevar el cuerpo a su posición original.

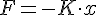    (1.13)

donde F es la fuerza elástica que aparece para devolver al cuerpo a su posición inicial; K es la constante de proporcionalidad, o constante elástica del muelle, y x es la distancia que separo al cuerpo de su posición inicial. Observamos que cuanto mayor sea la distancia que se separa el cuerpo del origen, mayor será la fuerza elástica que tiene que ejercer el muelle para devolverlo al origen.

En la ecuación 1.13 sustituimos la fuerza por su definición según la segunda ley de Newton y la aceleración es la derivada segunda del espacio respecto al tiempo, y llegamos a la ecuación:

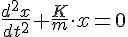    (1.14)

La solución de la ecuación 1.14 es:

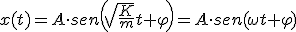    (1.15)

donde:

• A, es la amplitud, distancia máxima que el cuerpo se separa de su posición de equilibrio, se mide en metro.
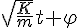• , es la fase del movimiento en el instante t, medido en radian.
• φ, es la fase inicial, la fase en t = 0, la posición del móvil antes de empezar el movimiento, en radian.
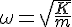• , es la frecuencia angular, cuyas unidades son rad·s^–1.

Por lo tanto, el movimiento de un cuerpo unido a un muelle sin masa que cumpla la ley de Hooke realiza un movimiento armónico simple. Como tal movimiento armónico es periódico, es decir, después de un tiempo igual al periodo todos los valores de posición, velocidad y aceleración serán iguales:

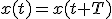    (1.11)

Despejando podemos definir el periodo como:

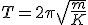    (1.16)

Encontramos que el periodo no depende del tiempo sino de la masa del cuerpo y la constante elástica del muelle, por lo que podemos decir que el muelle realiza un movimiento isócrono.