Cuando un cuerpo realiza un movimiento armónico simple, y se encuentra en la posición más alejada del punto central de la trayectoria, es decir, en la amplitud, durante un instante, el cuerpo no se mueve, es decir, toda la energía del cuerpo es energía potencial, Ep.
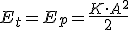(1.20)
donde K es la constante elástica del medio, definida por la ley de Hooke.
El cuerpo intenta recuperar su posición de equilibrio en el centro de la trayectoria y empieza a moverse, durante el movimiento el cuerpo además de la energía potencial debida a su posición tiene energía cinética, Ec, debida a su movimiento.
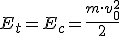(1.21)
el subíndice de la velocidad indica únicamente que es la velocidad del cuerpo al pasar por el origen de coordenadas, y, por tanto, es la velocidad máxima.
El sistema es conservativo, es decir, que la energía total del sistema se mantiene constante a lo largo del tiempo, lo que indica que cuando el cuerpo se encuentra en la posición más alejada del origen, la energía total es energía potencial, mientras que cuando pasa por el origen toda la energía es cinética. En cualquier punto intermedio la energía total será la suma de la energía potencial y cinética.
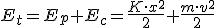(1.22)
Ahora, se introduce el espacio recorrido por un cuerpo que describe un movimiento armónico simple, ecuación 1.17, y la velocidad del mismo, ecuación 1.18, se puede calcular le energía del movimiento armónico simple:
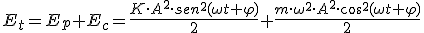(1.23)
Energía debida a la posición del cuerpo. Trabajo que el cuerpo puede realizar.