Una onda es la propagación de una perturbación en un medio material. Los sucesivos puntos del medio oscilarán sobre su posición de equilibrio pero no se trasladarán, por lo que una onda es la transmisión de energía sin transporte de materia.

En un medio material se puede propagar cualquier magnitud como la presión, o la energía, o la densidad o cualquier otro, a la que denominamos Ψ. Podemos calcular el valor de esa magnitud en cualquier punto del medio alejado del foco y en cualquier instante según la siguiente ecuación:

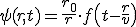    (1.24)

donde:

• r₀, es el tamaño del foco.
• r, es la distancia que separa el punto del medio y el foco.
• v, es la velocidad con la que la energía del movimiento ondulatorio se transmite por el medio, que no hay que confundir con la velocidad a la que oscila cada punto del medio que se mueve con un movimiento armónico simple.

A medida que nos alejamos del foco el cociente entre el radio del foco, r₀, que no aumenta con el tiempo, y la distancia a la que se encuentra el punto, r, se va haciendo cada vez más pequeño, y lo podemos considerar como constante. Si sólo consideramos el movimiento de la onda en uno de los ejes de coordenadas:

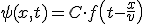     (1.25)

La ecuación 1.25 es la ecuación de una onda plana, sólo se desplaza en uno de los ejes de coordenadas, y tienen la particularidad de que todos los puntos afectados por esta onda se mueven a la vez, es decir, están en fase. A este plano se le conoce como frente de onda.

Tomamos derivadas parciales de la ecuación 1.25 respecto a cada una de las variables de la magnitud que se propaga como una onda, es decir, el espacio y el tiempo, y reordenamos:

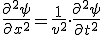    (1.26)

Hemos encontrado la ecuación general de las ondas planas o ecuación de D’Alembert, que se puede generalizar al espacio tridimensional:

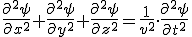    (1.27)