Para calcular la velocidad de propagación del sonido en el aire utilizaremos la fórmula de Laplace:

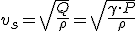    (1.37)

donde:

• Q, es el módulo de compresibilidad adiabático. En los gases, debido a la rapidez de las compresiones y expansiones, no da tiempo al intercambio de calor, y por lo tanto, no se modifica de la temperatura. En los gases es el producto entre el coeficiente adiabático, γ, y la presión.
• γ, es el coeficiente adiabático, es la relación entre los calores específicos a presión constante y a volumen constante del gas. Este coeficiente tiene un valor de 1,4 para el aire a las temperaturas ambientales:
  
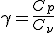      (1.38)
• p, es la presión del gas en el que se propaga la onda sonora.
• ρ, es la densidad del gas.

Consideremos que el gas en el que se propaga la onda sonora se comporta como un gas ideal y hagamos la correspondiente sustitución en la ecuación 1.30:

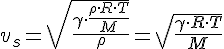    (1.39)

donde:

• R, es la constante universal de los gases, R = 8,314 462 618 153 24 J·mol^–1·K^–1.
• M, es la masa molar del gas. En el caso del aire atmosférico seco, M = 0,028964 kg·mol^–1.
• T, es la temperatura absoluta, T / K = 273,15 + t / ºC.

Del estudio de la ecuación 1.35 se desprende que la velocidad de propagación del sonido es función de la temperatura, a medida que la temperatura es cada vez más alta mayor es la velocidad de propagación del sonido.

Si una fuente de sonido se mueve en el seno del material en el que se propaga el sonido a una velocidad superior a la del sonido en ese medio, se produce lo que se llama una onda Mach, se ha roto la barrera del sonido, que se puede describir mediante el número de Mach:

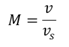 (1.40)

Y, dependiendo del valor obtenido para M se clasifican las velocidades de la siguiente manera:

•          M < 0,7 velocidad subsónica
• 0,7 ≤ M < 1,2 velocidad transónica
• 1,2 ≤ M < 5,0 velocidad supersónica
• 5,0 ≤ M          velocidad hipersónica