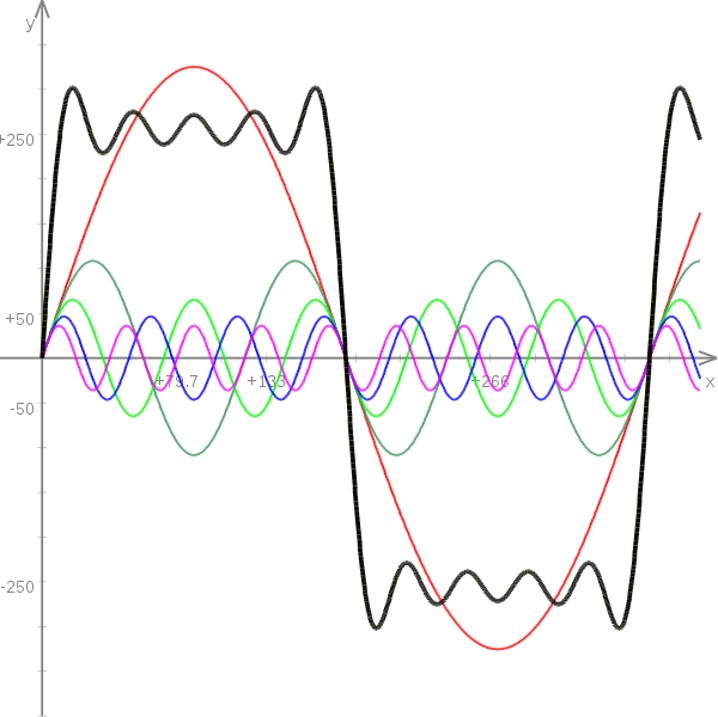
Cualquier función periódica Ψ(t), no necesariamente armónica, que sea continua, y cuya derivada también lo sea se puede descomponer en una suma infinita de funciones armónicas, mediante el desarrollo en serie de Fourier. Si la función Ψ(t) tiene un periodo T, esto quiere decir que el valor de la función se repite cada vez que transcurre un periodo de tiempo:
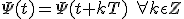 (2.1)
(2.1)El desarrollo en serie de Fourier permite expresarla como una suma infinita de senos y cosenos:
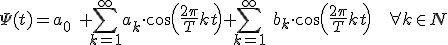 (2.2)
(2.2)donde:
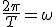 es la frecuencia angular fundamental de la señal y en consecuencia kω representa el k–ésimo armónico de la frecuencia fundamental. Con la condición de que:
es la frecuencia angular fundamental de la señal y en consecuencia kω representa el k–ésimo armónico de la frecuencia fundamental. Con la condición de que:
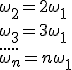
| Frecuencia | Longitud de onda | |
|---|---|---|
| Fundamental | υ | λ |
| Primer armónico | 2υ | λ/2 |
| Segundo armónico | 3υ | λ/3 |
| ... | ... | ... |
| n–ésimo armónico | nυ | λ/n |
Los coeficientes que aparecen en la ecuación 2.2 son las incógnitas que hay que calcular:
- a0, es el valor medio de la señal periódica Ψ(t) sobre un periodo:
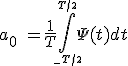 (2.3)
(2.3) - ak y bk representan las amplitudes desconocidas de los términos coseno y seno que se pueden calcular mediante las expresiones:
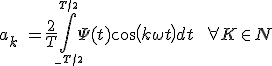 (2.4)
(2.4)
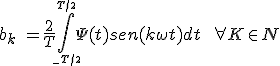 (2.5)
(2.5) - Este desarrollo en serie permite obtener el espectro de una señal, que describe el contenido frecuencial de dicha señal. Es decir, todo movimiento periódico está formado por su frecuencia fundamental, el primer elemento de la serie, y sus diversos armónicos, el resto de elementos de la serie.