Supongamos una onda plana que penetra en un tubo, por un extremo abierto del mismo, cuando la onda llega al final del tubo, rebota con la pared perpendicular del fondo y la onda vuelve, onda reflejada, por el mismo camino, encontrándose con la onda incidente en el interior del tubo e interaccionando con ella. Cada punto del interior del tubo se verá perturbado por las dos ondas simultáneamente.
Sea Ψi(x, t) la onda incidente, y Ψr(x, t) la onda reflejada, cuyas ecuaciones son las siguientes:
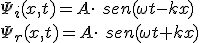 (2.6)
(2.6)Se considera que la fase inicial, φ, en ambas ecuaciones es cero para facilitar los cálculos. Se observa que las ecuaciones son en todo iguales excepto en el signo que indica que la onda reflejada vuelve en sentido contrario al que entró en el tubo. En cada uno de los puntos perturbados por ambas ondas el resultado será la suma de ambas perturbaciones:
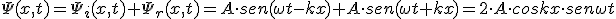 (2.7)
(2.7)La ecuación 2.7 es la ecuación de una estacionaria, esto quiere decir que es una onda que no se propaga ya que en los argumentos de las funciones armónicas no aparecen expresiones del tipo x ± vt. En las estacionarias la amplitud es dependiente de la posición de la partícula, que realizará un movimiento armónico simple con esa amplitud, siempre la misma. Si nos fijamos en la ecuación de la estacionaria, se observa que lo que multiplica a la función seno es la amplitud, tomemos el mismo criterio para las estacionarias y establezcamos que lo que multiplica a la función seno es la amplitud de la onda estacionaria, Aest, en esa posición:
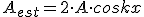 (2.8)
(2.8)Cuando cos(kx) = ±1 la amplitud de la estacionaria alcanza su valor máximo, son los vientres y los puntos del espacio en los que se vas a encontrar estos vientres deben cumplir la siguiente ecuación:
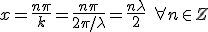 (2.9)
(2.9)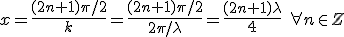 (2.10)
(2.10)Observamos la ausencia de los armónicos pares, y las frecuencias de cada modo:
A la frecuencia de número más bajo, se le denomina frecuencia fundamental de vibración del tubo, y las demás frecuencias, más agudas, corresponden a los armónicos.
En el caso de que el tubo tuviera los dos extremos abiertos entonces en ambos extremos se formarían vientres, o los dos extremos cerrados, se formarían nodos, como en la figura. La distancia entre dos nodos o dos vientres consecutivos es la mitad de la longitud de onda, encontramos que las longitudes de onda de cada modo de vibración deben cumplir:
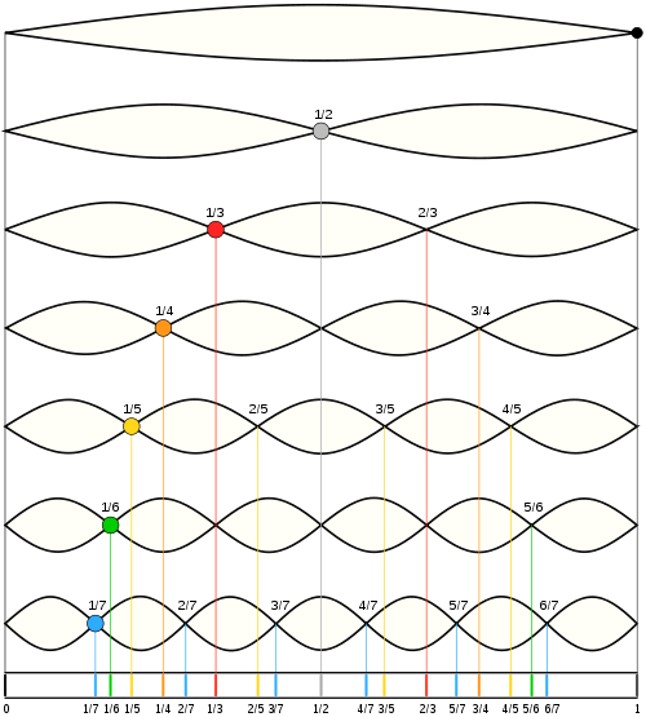
Resultado de la superposición de dos ondas que se propagan en sentidos opuestos.
En una estacionaria son los puntos que no se mueven a lo largo del tiempo.
Vientre: en una estacionaria el punto que vibra con la máxima elongación, a lo largo del tiempo.