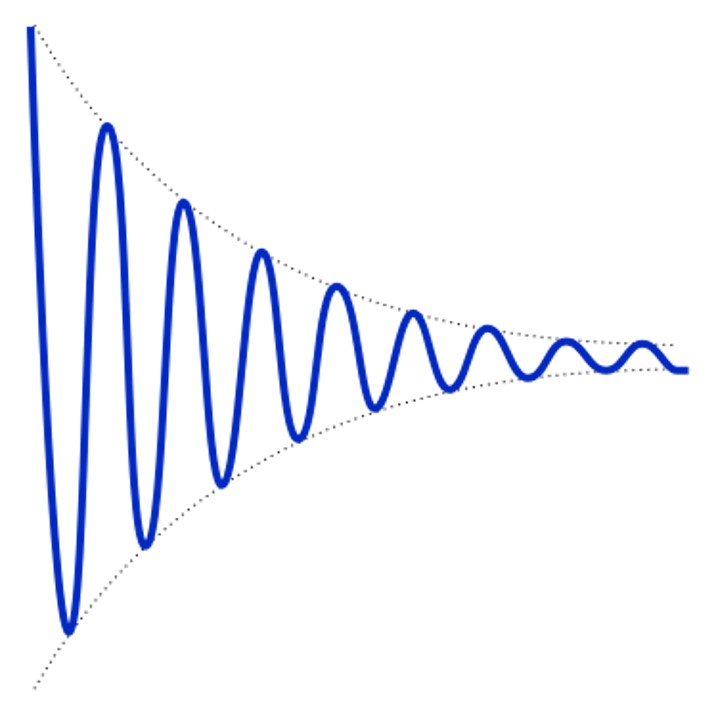
Cuando un punto material vibra con un movimiento armónico simple vimos en la unidad 1 que este movimiento se propagaba por todo el medio. Esto sería así si no se produjeran algunos factores que provocan que por un lado el foco llegue a pararse, y por tanto a dejar de emitir, y por otro que a medida que me alejo del mismo la vibración sea cada vez más pequeña hasta desaparecer como la vibración térmica propia de la temperatura a la que se encuentre el medio.
• Amortiguamiento del foco
La partícula perturbada en primer lugar, el foco de la onda, al desplazarse de su posición de equilibrio roza con las partículas de alrededor. La consecuencia de este rozamiento es que se pierde energía en forma de calor. Supongamos que en un tiempo dt, la partícula del foco pierde una cantidad de energía dE, que será proporcional a su energía inicial:
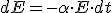(2.24)donde α es el coeficiente de amortiguamiento del foco y sus unidades son inverso de tiempo. Al integrar esta ecuación y considerando que en el instante t = 0 la energía de la partícula sea E0:
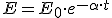(2.25)Y si tenemos en cuenta que la amplitud del movimiento del foco está relacionada con la energía, encontramos que:
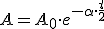(2.26)La consecuencia de todo esto es que al cabo de un tiempo la amplitud de la vibración es lo suficientemente pequeña como para ser indistinguible de la vibración producida por los movimientos térmicos del medio, momento en el que el foco deja de emitir.
• Atenuación por la distancia.
Ya vimos en la unidad 1 cómo a medida que nos alejamos del foco la intensidad de las ondas va disminuyendo. En el caso de las ondas planas no se produce esta disminución. En el caso de las ondas esféricas se va produciendo una disminución de la amplitud de la onda que es inversamente proporcional a la distancia al foco:
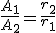(2.27)Y en el caso de las ondas cilíndricas la disminución de la amplitud es inversamente proporcional a la raíz cuadrada de la distancia al foco:
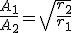(2.28)
• Absorción por el medio.
El medio, debido al rozamiento producido por la vibración de las partículas que se van viendo perturbadas por la onda, va absorbiendo parte de la energía de la onda y disipándola en forma de calor, de forma que llega un momento en el que la amplitud de la onda no se distingue de la vibración de origen térmico. Sea la disminución de la intensidad de la onda debida a este fenómeno dI, que será proporcional a la intensidad inicial de la onda, en el espacio recorrido dx:
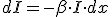(2.29)donde β es el coeficiente de absorción , cuyas unidades son inverso de distancia. Al integrar obtenemos la siguiente expresión:
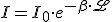(2.30)donde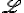 
es el espesor del medio atravesado por la onda, e I0 es la intensidad de la onda en el foco.
