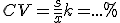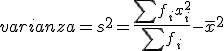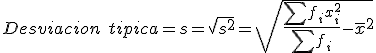Hay bastantes parámetros pero sólo vamos a estudiar el recorrido o rango y la desviación típica que se usan bastante. La varianza sólo la presentamos como un paso intermedio para la obtención de la desviación típica, y vamos a intentar usar solo una de las distintas fórmulas de cálculo.
Amplitud, rango o recorrido (R): Es la diferencia entre el mayor y el menor valor que toma la variable estadística (observaciones extremas). Sirve para valorar entre que valores se mueve la distribución.
Varianza (S2, б2 o sigma2): Es un parámetro que mide la distancia existente entre los valores de la serie y la media. Es la media aritmética de los cuadrados de las desviaciones respecto a la media. La varianza siempre será mayor que cero. Cuanto más se aproxima a cero, más concentrados están los valores de la serie alrededor de la media, y por el contrario, mientras mayor sea la varianza, más dispersos están.
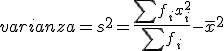
Desviación típica o estándar (б; S o sigma): Es la raíz cuadrada positiva de la varianza. Es una medida que expresa, en las mismas unidades de la variable (puntos, porcentajes, kilos, metros...) lo que se separan los datos de los valores centrales. Al igual que en el caso de la varianza, cuando más pequeña es más próximos están los datos al valor de la media. Para su cálculo vamos a utilizar la fórmula más sencilla.
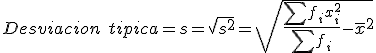
El coeficiente de variación (CV), que se define como la relación existente entre la desviación típica y la media. Expresa la variabilidad de los datos de una distribución y se dice que cuanto más pequeño sea, más útil será la distribución para trabajar con ella, e incluso cuando es mayor de un 33%, se considera que la distribución es poco homogénea, poco uniforme, muy dispersa y poco útil.