Estas medidas son usadas habitualmente y seguro que las conoces. Por ejemplo, imagina que has hecho dos exámenes en un módulo y has tenido un 7 y un 9. ¿Qué nota crees que te corresponde? Para responder a esto es posible que hayas calculado la “media” y digas que tienes un 8. O tal vez alguien te pregunte cuál ha sido la nota que más gente ha sacado, en este caso le responderás usando la “moda”.

Las medidas de centralización o promedios son parámetros o números que miden la tendencia central de los datos y expresan los valores centrales hacia los que los datos parecen agruparse. Son la media, la mediana y la moda.

La media aritmética (x) es la suma de todos los valores de una variable dividida por el número de valores estudiados. La media es el parámetro más utilizado ya que tiene en cuenta todos los datos y el cálculo resulta sencillo.

Es única y no sirve para variables cualitativas ni para datos con intervalos abiertos.

Para su cálculo se utiliza la siguiente fórmula:

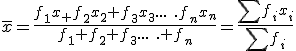
En los casos sencillos es fácil entender como se hace. Piensa por ejemplo que estamos estudiando el número de ausencias de piezas dentales en un grupo pequeño de pacientes (10 personas). Hemos obtenido los siguientes datos: 1, 3, 1, 4, 2, 5, 3, 3, 1, 5.

Si tuvieras que hacer la media de las ausencias, sumarías todos los valores y los dividirías entre los10 pacientes estudiados, ¿no? Harías: 1 + 3 + 1 + 4… o sea 28 / 10. Es decir, la media de ausencias en este grupo es de 2,8.

Usando una fórmula matemática y teniendo en cuenta que hay valores que se repiten, esto se podría expresar así:

En este caso es sencillo identificar los cuatro valores que toma la variable y los que se repiten porque son 10 personas, pero ¿si fueran 1.000 o 100.000? No sería posible, por lo que cuando hay muchos datos se necesita ordenarlos y una tabla en la que hacerlo.