Anexo I.- Ejercicios resueltos de cálculo de parámetros.

En este documento puedes revisar lo que has hecho. Hemos optado por poner la tabla al principio y hemos ido añadiendo las columnas según se han ido necesitando. Acuérdate de poner las unidades, que en este caso del IR son porcentajes (%), no lo confundas con la columna de porcentajes e intenta explicar los resultados.

  1. Ordena los datos en una tabla y calcula las frecuencias.
    • Serían las seis columnas: xi, fi, fr %, F, Fr y %a de la tabla.
      Índice de restauración

      		xi fi fr % F Fr %a xifi fixi2
      0-10 5 0 0 0 0 0 0 0 0
      10-20 15 2 0,025 2,5 2 0,025 2,5 30 450
      20-30 25 5 0,062 6,2 7 0,087 8,7 125 3.125
      30-40 35 9 0,112 112 16 0,199 19,9 315 11.025
      40-50 45 13 0,162 16,2 29 0,361 36,1 585 26.325
      50-60 55 19 0,237 23,7 48 0,598 59,8 1.045 57.475
      60-70 65 11 0,137 13,7 59 0,735 73,5 715 46.475
      70-80 75 13 0,162 16,2 72 0,897 89,7 975 73.125
      80-90 85 5 0,062 6,2 77 0,959 95,9 425 36.125
      90-100 95 3 0,037 3,7 80 0,996 (aprox = 1) 99,6 (aprox = 100) 285 27.075
            80 1 100        
  2. ¿Cuánta gente ha tenido un IR entre 80 y 90%?
    • 5 personas.
  3. ¿Cuánta gente ha tenido un IR entre 80 y 90% o menos?
    • 77 personas.
  4. ¿Qué porcentaje de personas han tenido un IR de entre 0 y 10%?
    • Nadie, 0%.
  5. ¿Qué porcentaje de gente ha tenido un IR de 50% o menos?
    • 36,1%.
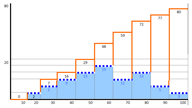
  6. Representa los datos de la frecuencia absoluta y de la frecuencia absoluta acumulada en un gráfico.
    Histogramas de frecuencias absolutas y de frecuencias absolutas acumuladas.
  7. ¿Qué media de índice de restauración corresponde a este pueblo?

    La media es igual al cociente entre el sumatorio del producto de f sub i y c sub i, y el sumatorio de f sub i, todo ello igual a 4.500 entre 80. La media igual a 56,25.

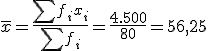
    • Es decir, poniendo la unidad e interpretando la cifra obtenida, la media del índice de restauración es del 56,25% en este pueblo.
  8. ¿Qué valor ha sido el más frecuente? Calcúlalo.
    • La frecuencia absoluta más alta es 19, que corresponde al intervalo 50-60.

      X sub o es igual a L sub i (límite inferior del intervalo modal) más el producto de c (la amplitud del intervalo) por la fracción de D sub 1 (diferencia entre la frecuencia absoluta de la clase modal y de la clase inmediatamente anterior) entre la suma de D sub 1 (diferencia entre la frecuencia absoluta de la clase modal y de la clase inmediatamente anterior) y D sub 2 (diferencia entre la frecuencia absoluta de la clase modal y de la clase siguiente). En este caso, la moda es igual a 50 más el producto de 10 por la fracción de 6 entre la suma de 8 más 8. Es decir la moda es igual a 54,28.

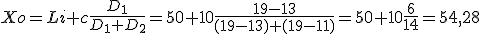
    • Es decir, poniendo la unidad e interpretando la cifra obtenida, el valor del índice de restauración que más se repite, es el 54,28%.
  9. Se va a seleccionar al 40% de la gente que menos tratada tiene la boca para dar un curso de prevención. ¿Con que parámetro se haría? Calcúlalo.
    • Se trata de seleccionar a un 40% de gente que tiene la boca menos tratada, por tanto con un IR más bajo. Por ello, se empieza a coger desde la izquierda-los valores más bajos en un eje de representación se colocan a la izquierda y los más altos a la derecha-. El parámetro a calcular es por tanto el P40.
    • Para el cálculo del P40: F debe ser mayor de:

      F mayúscula ha de ser mayor del cociente 80 y100, multiplicado todo ello por 40, es decir mayor que 32.

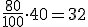
    • Observando en la tabla la columna F, eso sucede con el número 48, que corresponde al intervalo 50-60.
    • Aplicando la fórmula para calcular el valor:

      El percentil 40 es igual a 50 más el producto de 10 por la fracción en cuyo numerador está la diferencia entre el producto de la fracción 80 partido 100, multiplicado por 40 y 29, y en cuyo denominador está el 19. Es decir, el P sub 40 es igual a 51,57.

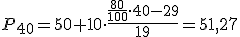
    • Es decir, seleccionaremos para el curso a las personas que tengan un índice de restauración menor del 51,57% (eran las personas con la boca menos tratada).
  10. Se quiere seleccionar también a un 10% de las personas con el IR más alto, para hacer una revisión y un seguimiento durante unos años. ¿Qué parámetro se usaría?
    • En este caso se trata de seleccionar al 10% con la boca más tratada, por lo que se empieza a coger desde la derecha -los valores más bajos en un eje de representación se colocan a la izquierda y los más altos a la derecha-.
    • Este 10% corresponde al P90. Fíjate en la imagen que se adjunta, puede ayudarte.
    Barra que expresa como decidir el percentil a calcular.
  11. Calcula la desviación típica y relaciónala con la media aritmética.

    S igual a la raíz cuadrada de s2 o de la varianza. Es decir, s es igual a la raíz cuadrada de la diferencia entre el cociente entre el sumatorio del producto de f minúscula sub i por el cuadrado de x sub i dividido por el sumatorio de f minúscula sub i, y el cuadrado de la media aritmética.

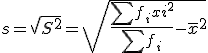
    Sustituyendo los valores en la fórmula:

    La desviación típica es igual a la raíz cuadrada del cociente de 281.200 entre 80, menos el cuadrado de 56,25. Esto es igual a la raíz cuadrada de 3.515 menos 3.164,06, igual todo ello a la raíz cuadrada de 350,94. La desviación típica es igual a 18,73.

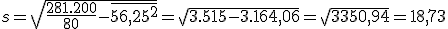
  12. ¿Es esta una distribución homogénea?

    CV es igual al cociente de s (desviación típica) entre x ̅ (media aritmética),multiplicado por un coeficiente 100. CV es igual al cociente de18,73 y 56,25 multiplicado por el coeficiente 100. Es decir, es igual a 33,29%.

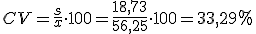
    • La variabilidad de esta distribución de datos es de un 33,29%. ¿Es mucho o poco? Se puede decir que está en el límite que es del 33%.
  13. ¿Entre que dos valores se encontrarán probablemente el 65 % de los datos?
    • Se sabe que en la mayoría de estas series de datos estos tienden a adoptar una forma determinada, que se le suele llamar campana de Gauss. Por ello se sabe que es probable que el 68% de los dato estén entre x-1s y x+1s.
    • En este caso 74,98 y 37,52% del IR.

EJERCICIO RESUELTO SOBRE CORRELACIÓN

Índice de correlación de 0,97:

  • Es positivo, por tanto la correlación es directa. Esto significa que a aumentos de una de las variables, corresponden aumentos de la otra. En este caso, que cuando aumenta la tasa del consumo de bebidas azucaradas en estos pueblos, aumenta la tasa de caries.
  • Es un valor muy próximo a [1], por tanto es fuerte, o lo que es lo mismo, una de las variables depende mucho de la otra. En este caso la tasa de caries depende mucho del consumo de estas bebidas.

Índice de correlación de 0,17:

  • En este caso también es positivo, por tanto cuanto más ausencia de cepillado (lo que en un lenguaje coloquial diríamos a menos cepillado) más caries.
  • En un valor próximo a 0, por tanto la correlación es débil, por lo que la caries en estos pueblos no depende mucho de la ausencia de cepillado.

Ambos índices:

  • Según este estudio, la correlación entre caries y consumo de bebidas azucaradas es más fuerte que entre caries y ausencia de cepillado, por que el valor obtenido está próximo a [1], mientras que la otra el valor es 0,17, más próximo a 0.
  • Es decir la variable caries depende más del consumo de bebidas azucaradas.
  • Aunque no lo pregunta en el ejercicio, se podría añadir, que en caso de un programa de educación para la salud, para controlar la caries, se debería hacer sobre el consumo de bebidas azucaradas, y no sobre el cepillado, porque según este estudio la caries depende más de ello.