El recuento en cámara se basa en determinar el número de hematíes en un pequeño volumen de dilución y realizar los cálculos adecuados, teniendo en cuenta el volumen contado y el factor de dilución aplicado a la muestra, para obtener el número de hematíes de la muestra en el volumen utilizado como unidad de medida. Estas unidades de medida son, generalmente, el número de hematíes por milímetro cúbico (mm³) o, número de hematíes por litro (L).

Para entender todo esto es necesario saber cómo funciona y cuáles son las características de una cámara de Neubauer mejorada.

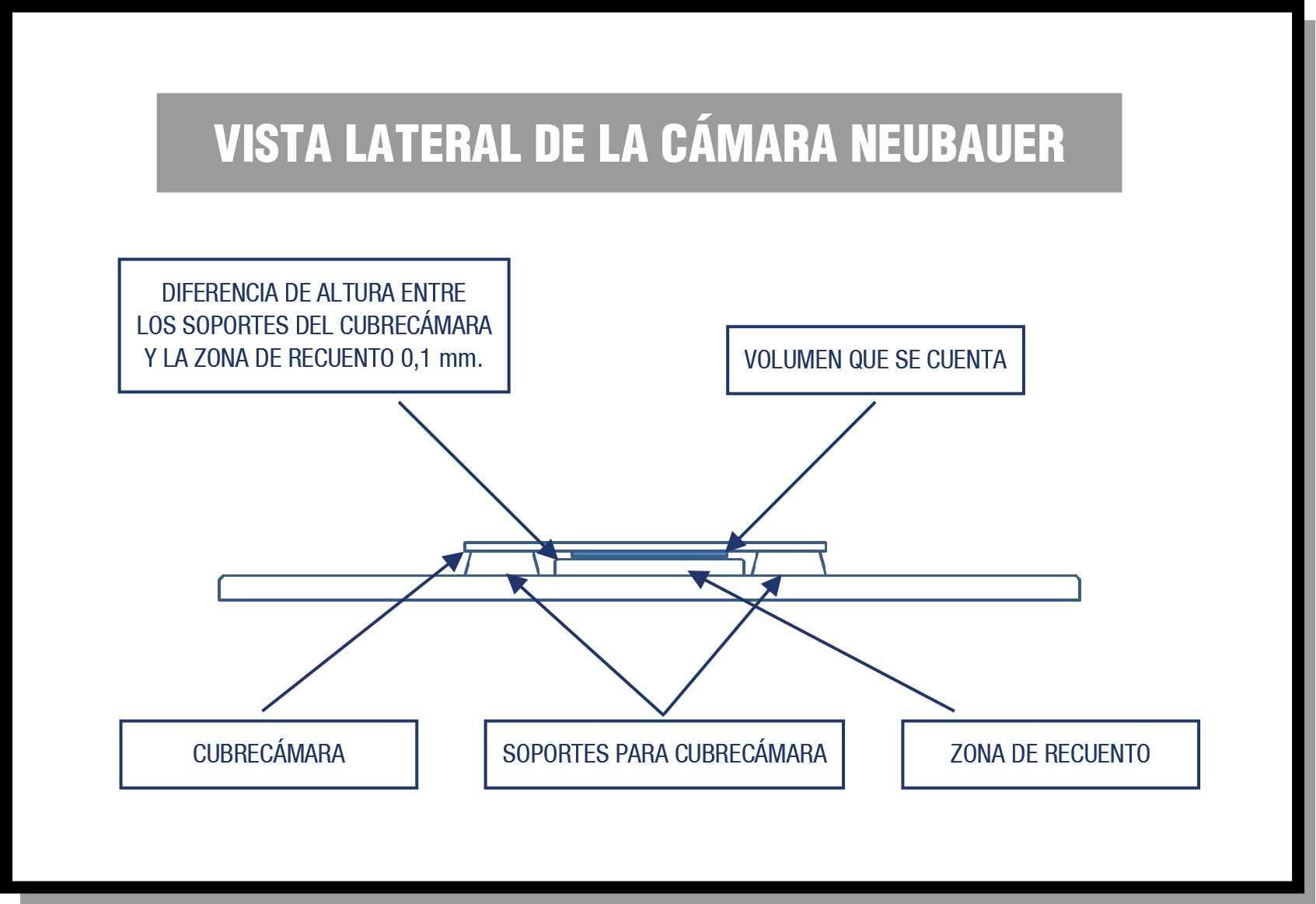
La cámara es una pieza de vidrio rectangular algo más grande que un portaobjetos y de mayor grosor a la que se le han practicado una serie de hendiduras horizontales y verticales de manera que se delimitan dos zonas de recuento. En dichas zonas se ha grabado sobre el vidrio una cuadrícula de dimensiones conocidas. Estas zonas de recuento están limitadas lateralmente por dos barreras o plataformas más altas (0,1 mm) que las primeras. Es sobre estas plataformas donde se fija el cubrecámara creándose un pequeño espacio con forma prisma cuadrangular (entre la superficie de la zona de recuento y el cubrecámara) de altura 0,1 mm.

 

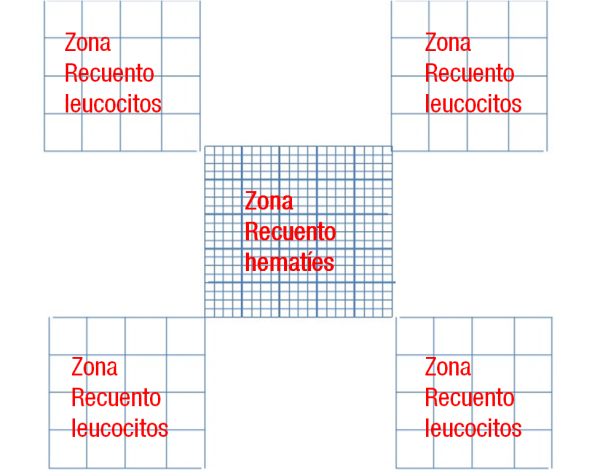
La zona de llenado de la cámara corresponde con el área de la cuadrícula de recuento, que es de 9 mm², es decir, 3 x 3 mm. La cuadrícula de recuento tiene, a su vez, 9 cuadrículas grandes de 1 mm². El cuadrado grande central está divido en 25 más medianos (divididos por tres líneas muy próximas, que nos sirven de referencia para evitar confusiones con las líneas simples que dividen estos cuadrados medianos en 16 cuadrados pequeños, cada uno).

                                                               

 

La fórmula general para el recuento celular es:

Recuento = (Células contadas x factor de dilución) / Área (mm²) x Profunidad (0.1) = nº de células / mm³

Se puede deducir las dimensiones de cada uno de los cuadrados, resolviendo las siguientes cuestiones:

• ¿Qué superficie tiene la cuadrícula de recuento de hematíes? 

Se trata de un cuadrado que tiene de lado 1 mm, por tanto, aplicando la fórmula: Superficie = Lado • Lado, sustituye por sus valores, , por tanto la superficie es 1 mm².

• ¿Qué superficie tiene cada uno de los 25 cuadrados medianos? 

Primero, se halla el valor de su lado. El lado de la cuadrícula completa mide 1 mm. y esta se divide en 5 partes iguales (cada uno de los lados de los cuadrados medianos), implica que dividiendo 1 mm entre 5 obtenemos el valor del lado de los cuadrados medianos 1mm/5 = 0,2 mm; y aplicando la fórmula anterior: .

• ¿Qué superficie tiene cada uno de los 16 cuadrados pequeños que tiene un cuadrado mediano? 

Siguiendo la misma forma de proceder, si se divide el valor del lado de un cuadrado mediano entre 4 obtendremos el valor del lado de un cuadrado pequeño, es decir, 0,2 mm/4 = 0,05 mm, y aplicando la fórmula de la superficie. Superficie = 0,05 mm • 0,05 mm = 0,0025 mm².