Sistema binario. El bit y el byte.
Sistema binario
En nuestro lenguaje utilizamos cifras y letras. En los números utilizamos el sistema decimal, llamado así porque utiliza 10 cifras distintas: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
El sistema binario utiliza dos cifras distintas: 0. 1. Un número binario puede ser 101110 pero no 101120 porque el dígito 2 no es admitido.
Los ordenadores sólo utilizan 0 y 1, por lo que utilizan el sistema binario.
Notación: Como el número 101110 existe tanto en binario como en decimal, se hace necesario cuando estamos utilizandos distintos sistemas utilizar una notación, de forma que anotaremos con un subíndice el sistema que estamos utilizando. Para binario utilizamos 1011102 y si fuera decimal 10111010
Bit y byte
El bit es un número binario con una única cifra. De forma que con un bit solo se puede escribir 0 o 1 y se anota por b. Hay 21 = 2 números distintos (del 0 al 1)
El byte va a ser un conjunto de 8 bits. Para entender cuántos números distintos se pueden escribir con 1 byte, seguimos el siguiente razonamiento:
- Con dos bit se puede escribir 00, 01, 10, 11. Hay 22 = 4 números distintos (del 0 al 3)
- Con tres bit se pueden escribir 000, 001, 010, 011, 100, 101, 110, 111. Hay 23 = 8 números distintos (del 0 al 7)
- Por tanto, con cada bit se doblan los números posibles a escribir. De esta forma estamos preparados para definir que es el byte.
El byte es un número binario de 8 cifras y se anota por B. Al ser 8 cifras, se pueden escribir 28 = 256 números distintos (del 0 al 255)
La importancia del byte se debe a que con un byte, se pueden representar 256 caracteres alfanuméricos distintos, que son necesarios para escribir cualquier texto en nuestro lenguaje. Si escribimos en el bloc de notas la palabra hola y lo guardamos como prueba.txt y miramos a continuación en propiedades cuánto ocupa el archivo veremos que ocupa 4 bytes. Esto se debe a que para cada letra se ha utilizado un byte (código ascii extendido).
Debido a esta equivalencia, muchas veces al byte se le identifica con carácter. De forma que se dice que el archivo prueba.txt ocupa 4 bytes o 4 caracteres.
Una pregunta sería porque hacen falta 1 byte para una letra. ¿Por qué hacen falta 8 bits que sirven para representar 256 caracteres distintos para una letra si sólo tenemos cerca de 30 letras en el abecedario? Hay que tener en cuenta que en nuestro lenguaje utilizamos el abecedario, pero tenemos distintas representaciones para las mayúsculas y las minúsculas, además tenemos vocales acentuadas y no acentuadas, también tenemos signos de puntuación y paréntesis; e incluso escribimos dígitos numéricos en nuestros textos y caracteres invisibles, llamados de control como el tabulador e intro.
Con vistas al cálculo de direcciones IP en las redes que vemos en el siguiente libro es muy importante recordar la idea de potencia vista aquí:
- Con 1 byte u 8 bits, se pueden representar 28=256 números distintos, del 0 al 255 (del 00000000 al 11111111)
- Con 16 bits, se pueden representar 216=65536 números distintos, del 0 al 65535 (del 0000000000000000 al 1111111111111111)
Conversión decimal a binario
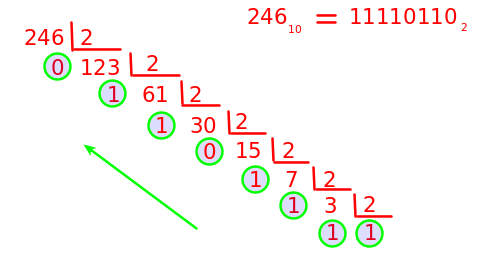
Para convertir un número decimal a binario, se realizan divisiones enteras por 2, utilizando el cociente entero para dividir de nuevo por 2, hasta que el cociente sea 0 o 1. Para obtener el número binario, coger como cifra más significativa el último cociente, y después todos los restos, empezando desde los últimos.
Conversión binario a decimal
Cada bit se multiplica por una potencia de 2, comenzando desde el bit menos significativo (por la derecha)Ejemplo: Convertir 111101102 a decimal
11110110= 0*20 + 1*21 + 1*22 + 0*23 + 1*24 + 1*25 + 1*26 + 1*27 =
= 0*1 + 1*2 + 1*4 + 0*8 + 1*16 + 1*32 + 1*64 + 1*128 =
= 2 + 4 + 16 + 32 + 64 + 128 = 246
Se obtiene 111101102 = 24610
El anterior proceso, se podría resumir en sumar la potencia de 2 correspondiente cuando el bit es 1, y no sumar nada cuando el bit es 0.
Aquí se refleja una tabla con 4 ejemplos de binario a decimal, utilizando este esquema.
|
Binario |
27 = 128 |
26 = 64 |
25 = 32 |
24 = 16 |
23 = 8 |
22 = 4 |
21 = 2 |
20 = 1 |
Suma |
Decimal |
|---|---|---|---|---|---|---|---|---|---|---|
|
00000000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0+0+0+0+0+0+0+0=0 |
0 |
|
10101100 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
128+32+8+4 |
172 |
|
00111110 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
32+16+8+4+2 |
62 |
|
11111111 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
128+64+32+16+8+4+2+1 |
255 |