El principio de Bernoulli, fue definido en el siglo XVIII por el matemático francés Daniel Bernouille, y supuso un gran avance en el campo de la hidrodinámica. Este principio determina que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido.
Al definir la conservación de la energía como fundamento del sistema se puede establecer que, cuando comparamos dos puntos del mismo, la energía contenida en el punto A y la energía contenida en el punto B deben ser la misma. Esto se conocer a su vez como el principio de conservación de la energía y permite relacionar todos los puntos de la red entre sí, comparando el balance energético existente entre varios de ellos.
Por lo tanto el principio d Bernoulli nos da dos claves para la interpretación de las redes hidrodinámicas. Si comparamos dos puntos de un sistema, podemos establecer que:
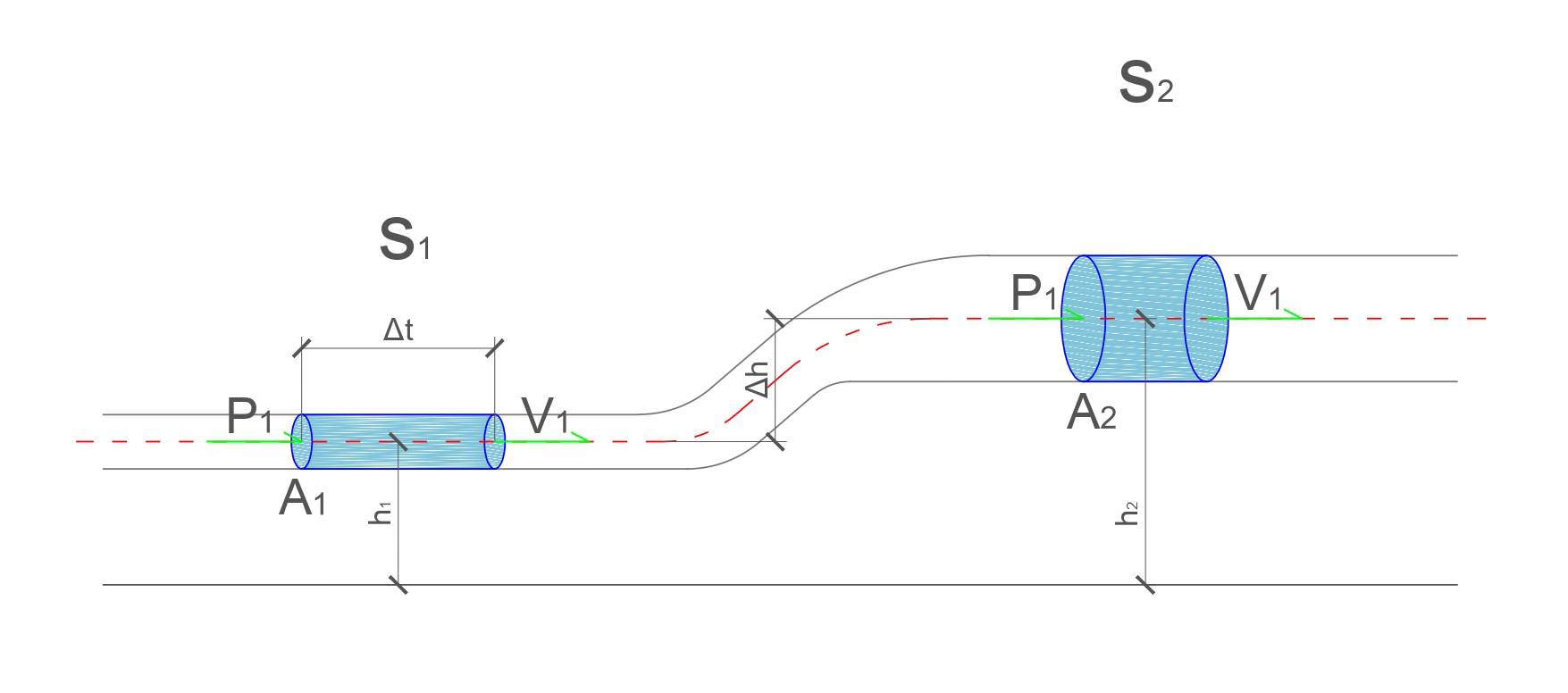
- La cantidad de masa de agua que circula por el punto S1, será la misma que circulará por el punto S2
- El balance energético del sistema es constante, por lo que la energía contenida en el punto A y la energía contenida en el punto B, son la misma, aunque tengan diferentes componentes.
Principio de conservación de la masa
Si analizamos el principio de Bernoulli desde el punto de vista de la conservación de la masa, como ya hemos mencionado, podemos concluir que:
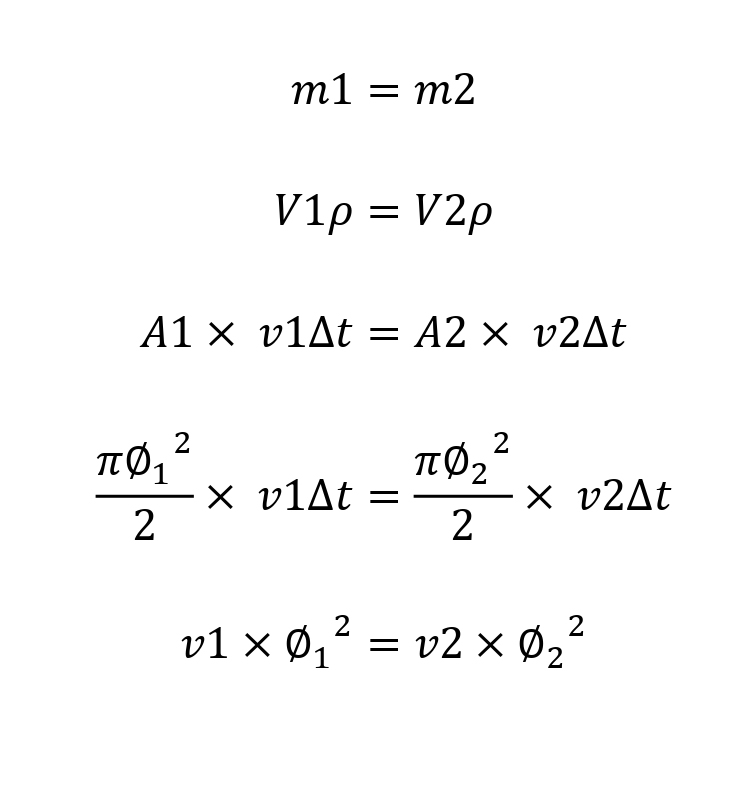
Partiendo del principio de conservación podemos decir que la masa del punto debe ser igual a la masa del punto 2. Para calcular esa masa, conociendo las dimensiones de la tubería, debemos multiplicar el volumen del cilindro 1 por su densidad y el volumen del cilindro 2 por su densidad. Al tener la misma densidad a ambos lados este componente desaparece y podemos concluir que el volumen del punto 1 debe ser igual al volumen del punto 2.
Como podemos ver en el diagrama para calcular el volumen de los cilindros debemos multiplicar la superficie A por la longitud. Aunque desconocemos la longitud exacta sabemos que será la velocidad del agua en cada punto multiplicada por la diferencia de tiempo que trascurre en el momento de la comparativa, que será la misma para el punto A y el punto B. En conclusión podemos establecer, simplificando la fórmula que, la superficie del punto 1 por su velocidad es igual a la superficie del punto 2 por su velocidad.
Por último vemos que esa superficie es una circunferencia y si dentro de la fórmula de la superficie de la circunferencia sustituimos el radio de la misma por la mitad del diámetro y simplificamos la fórmula, podemos concluir que la velocidad está relacionada con el cuadrado del diámetro. En conclusión se establece una relación indirecta entre el cuadrado del diámetro de la tubería y la velocidad de circulación del flujo. A más velocidad, menor diámetro y a menor velocidad, mayor diámetro
Principio de conservación de la energía
Si analizamos el principio de Bernouille desde le punto de vista de la conservación de la energía, como ya se ha mencionado, podemos concluir que:

Partiendo del principio de conservación de la energía, podemos decir que la energía contenida en el punto 1 y la contenida en el punto 2 son la misma. Si despreciamos los efectos de la energía térmica y analizamos sólo la energía mecánica de cada punto, veremos que en ambos puntos tenemos tres tipos de energía: energía cinética, energía potencial gravitatoria o de altura y energía potencia elástica o presión hidráulica. Mediante esta comparativa podemos analizar el valor de la energía en julios o en mca.
Los mca o metros de columna de agua es una unidad de energía que permite saber qué altura puede alcanzar un caudal de un fluido, en este caso agua, gracias a la energía potencial contenida en el mismo. Son muy empleados en cálculos de redes a presión por su fácil aplicación directa entre el cálculo y el diseño de la red. Si decimos que un flujo de agua tiene 5mca quiere decir que contiene energía suficiente para poder llegar (sin contemplar las pérdidas de carga) a los 5 metros de altura.
Para analizar la ecuación en mca debemos dividir todos los términos de ambos lados entre la mg (masa por gravedad), en el caso concreto de la Presión esto equivale a dividir la presión por el peso específico del fluido. De esta forma la ecuación queda muy simplificada y la energía potencial gravitatoria se puede interpretar directamente como la altura en metros, lo que nos ayuda enormemente al análisis de las redes desde el punto de vista de diseño.
La conclusión principal valorando que la altura de ambos puntos sea la misa es que la velocidad y la presión son indirectamente proporcionales, a mayor velocidad, menor presión. Si analizamos conjuntamente las conclusiones extraídas de los dos principios de conservación, vemos también que el diámetro se relaciona indirectamente con la presión, es decir a mayor diámetro, menor presión
Rama de la física que estudia el movimiento de los fluidos.
Propiedad de los fluidos que caracteriza su resistencia a fluir, debida al rozamiento entre sus moléculas.
Resistencia que se opone a la rotación o al deslizamiento de un cuerpo sobre otro.
La energía térmica (también energía calórica o energía calorífica) es la manifestación de la energía en forma de calor. En todos los materiales los átomos que forman sus moléculas están en continuo movimiento ya sea trasladándose o vibrando
La energía mecánica de un cuerpo o de un sistema físico es la suma de su energía cinética y la energía potencial. Se trata de una magnitud escalar relacionada con el movimiento de los cuerpos y con las fuerzas de origen mecánico, como son la fuerza gravitatoria y la de origen elástico, cuyo principal exponente es la ley de Hooke. Ambas son fuerzas conservativas. La energía mecánica asociada al movimiento de un cuerpo es la energía cinética, que depende de su masa y de su velocidad. En cambio, la energía mecánica de origen potencial o energía potencial, tiene su origen en las fuerzas conservativas, proviene del trabajo realizado por estas y depende de su masa y de su posición. El principio de conservación de la energía relaciona ambas energías y expresa que la suma de ambas energías, la energía potencial y la energía cinética de un cuerpo o un sistema físico, permanece constante. Dicha suma se conoce como la energía mecánica del cuerpo o del sistema físico.
Unidad de trabajo del sistema internacional, que equivale al trabajo producido por una fuerza de 1 newton cuyo punto de aplicación se desplaza 1 metro en la dirección de la fuerza. (Símb. J).
Un metro de columna de agua es una unidad de presión que equivale a la presión ejercida por una columna de agua pura de un metro de altura sobre la gravedad terrestre.
Se llama peso específico a la relación entre el peso de una sustancia y su volumen.