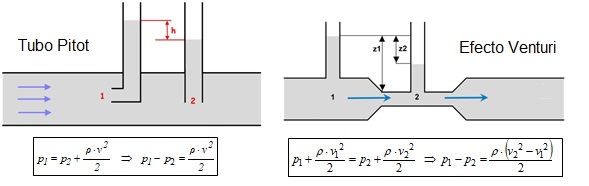
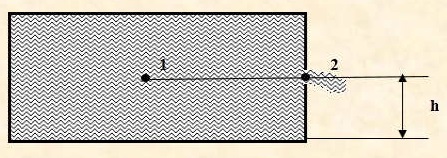
En un fluido ideal, que fluye sin rozamiento, la energía permanece constante a lo largo de su recorrido. Este principio es, en cierta forma, la aplicación a fluidos de la Ley de Conservación de la Energía. La energía de un fluido consta de dos partes: la energía térmica (que depende de su temperatura, calor específico, densidad y caudal) y la mecánica que, a su vez consta de los tres componentes siguientes:

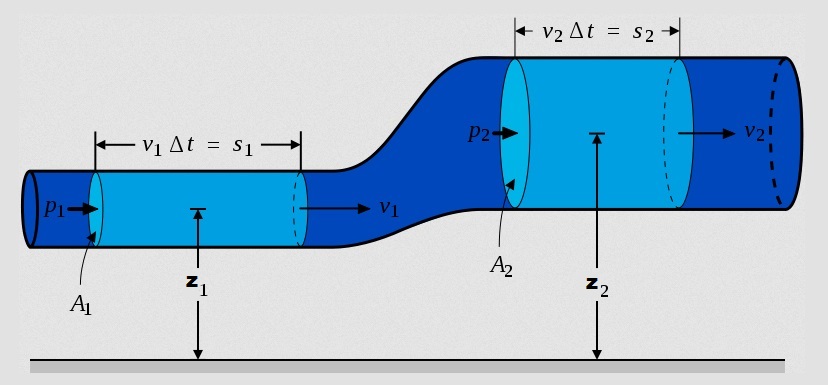
Cinética: es la energía debida a la velocidad que posea el fluido. Su variación, entre los puntos 1 y 2, viene dada por:

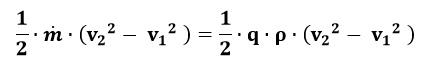
Potencial: es la energía debido a la altitud que un fluido posee. Su variación, entre los puntos 1 y 2, viene dada por:

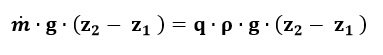
Energía de flujo: es la energía que un fluido contiene debido a la presión que posee. También se llama energía piezométrica. Su variación se expresa:

La suma de estas tres energías deberá permanecer constante, según la Ley de Conservación de la Energía. Dicho de otro modo, si en un punto aumenta su energía cinética es a costa de la disminución de alguna de las otras dos. Es como en una montaña rusa, cuando el vehículo está en lo alto tiene elevada energía potencial y baja energía cinética, mientras que al descender tiene poca energía potencial y elevada energía cinética. Por lo tanto, la suma de las variaciones de potencia mecánica anteriores ha de valer cero:

La ecuación de Bernouilli se puede poner de varias formas. Si sumamos las tres ecuaciones de las energías (potencial, cinética y piezométrica) y dividimos cada uno de los términos entre el caudal, obtendremos la ecuación (1). En la ecuación (2) se han igualado las energías en los dos puntos y aparecen tres términos en cada miembro de la igualdad, correspondientes a lo que podríamos denominar presión dinámica (relacionada con la energía cinética), presión relacionada con la altura y presión estática (la interna que tiene el fluido). En la tercera ecuación, después de dividir la ecuación (2) por ρ y g, obtenemos una ecuación parecida, pero el término libre es la altura. Ello significa que las tres energías están expresadas en metros de la columna de agua o, dicho de otro modo, en formato de energía potencial

Finalmente, si se toma el punto más bajo de la tubería como una altura de 0 m, la fórmula nos queda más simplificada:

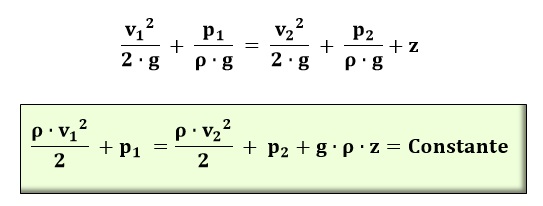
En el caso de que estemos ante una tubería horizontal, donde no hay desniveles (z= 0) tendremos:

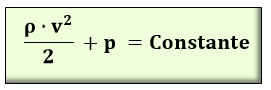
donde:

v = velocidad del fluido en la sección considerada (m/s)

g = aceleración gravitatoria (9,8 m/s²)

z = altura en la dirección de la gravedad desde una cota de referencia (m)

p = presión a lo largo de la línea de corriente (Pa).

ρ = densidad del fluido (kg/m³)