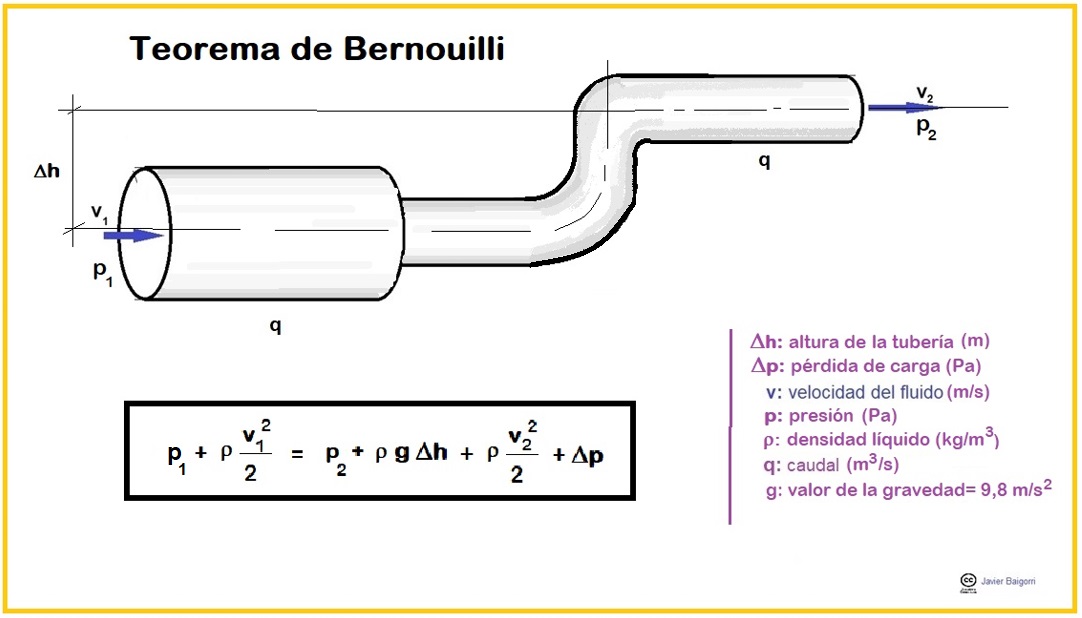
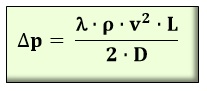Te habrás dado cuenta de que en el principio de Bernouilli se habla de un fluido perfecto sin rozamiento. En la realidad esto no sucede así. Los fluidos están compuestos por moléculas que chocan con las paredes de las tuberías, es decir, sufren un rozamiento. En un fluido real la presión disminuye a lo largo de la tubería por la que discurre, aunque la tubería sea horizontal y de sección uniforme, contrariamente a lo que hemos visto en el principio de Bernouilli. También puede observarse una disminución de presión después de pasar por un codo, una válvula o un estrechamiento.

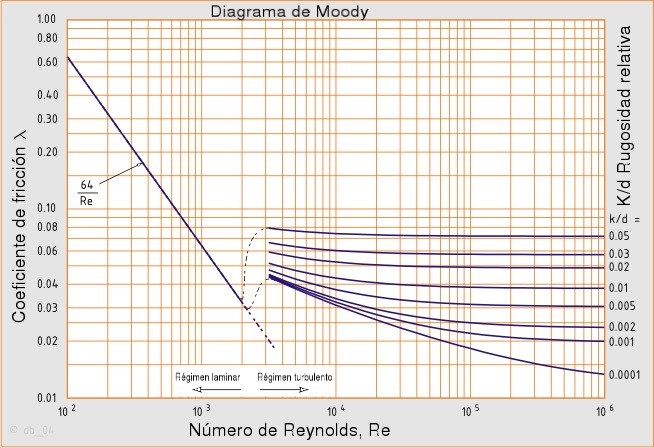
Un fluido real en movimiento sufre pérdidas de energía debidas al rozamiento contra las paredes de la tubería (pérdidas lineales) o por accidentes de recorrido (pérdidas singulares). Las pérdidas singulares se originan al generarse rozamiento y turbulencias. El número de Reynolds en una tubería lineal se calculaba con la fórmula vista en la que dependía de la viscosidad, densidad, diámetro y velocidad del fluido. Este número sirve, además de para determinar el régimen del flujo (laminar o turbulento) para calcular analíticamente las pérdidas por rozamiento en tuberías.

Las pérdidas de carga lineales se deben al rozamiento del fluido con las paredes de las tuberías. La pérdida de carga entre dos puntos separados por una longitud L en una tubería de diámetro D viene dada por:

Donde:

∆p: pérdida de carga (Pa)

λ: coeficiente adimensional llamado coeficiente de pérdida de carga lineal.

ρ: es la densidad (kg/m³)

v: velocidad del fluido (m/s)

L: longitud del tramo (m)

D: diámetro (m)

El cálculo de ese coeficiente λ es fundamental para obtener la pérdida de carga en la tubería. La forma de calcularlo depende del régimen del fluido. Para un régimen laminar:

El cálculo para el régimen turbulento es más complicado. En este caso tiene gran influencia la rugosidad de las paredes de la tubería y la magnitud de las turbulencias. Para determinar la pérdida se suelen utilizar ábacos, como el de Moody y fórmulas específicas para cada material.

Las pérdidas por accidentes son las que experimenta el fluido al dejar el tramo recto y enfrentarse a otros elementos de las tuberías como pueden ser codos, llaves, etc. Experimentalmente se ha visto que la pérdida de carga en un accidente viene dada por la siguiente expresión:

Donde

∆p: pérdida de carga (Pa)

ξ: coeficiente de singularidad

ρ: densidad (Kg/m³)

v: velocidad (m/s)

En este caso, tal como ocurre para las pérdidas lineales, la clave está en el valor de la constante adimensional ξ. Este valor se puede encontrar en distintas tablas. En el siguiente enlace tienes una tabla válida para diferentes fluidos, en donde podemos obtener la pérdida de carga de los elementos singulares:

Un método alternativo, más práctico, es el de la longitud equivalente. Este método consiste en relacionar cada accidente con una longitud equivalente de conducto recto del mismo diámetro. Esto facilita el cálculo al "linealizar" el conducto a calcular. Estas relaciones también se encuentran tabuladas. En el siguiente enlace puedes ver una tabla de longitudes equivalentes:

Más adelante en esta unidad utilizarás estas tablas para el cálculo de conductos y de tuberías.

Ecuación de Bernouilli con pérdidas de carga

La ecuación de Bernouilli que hemos visto la podemos completar teniendo en cuenta las pérdidas de carga totales en una tubería, tal como vemos en la imagen. Igualmente, clicando la imagen puedes descargarte una Hoja excel para facilitar los cálculos: