3.9.- Medidas de dispersión.
La varianza (S2) nos permite identificar la diferencia media que hay entre cada uno de los valores respecto a su punto central (X). Esta diferencia media es calculada, elevando cada una de las diferencias al cuadrado (con el fin de eliminar los signos negativos), y calculando su media aritmética; es decir, sumando todos los cuadrados de las diferencias de cada valor respecto a la media y dividiendo este resultado por el número de observaciones que se tengan.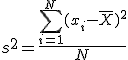
Donde representa la media de todos los valores y N representa el número de observaciones o el tamaño de la muestra.
Recomendación
Con frecuencia 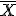 no es un número entero, entonces las desviaciones suelen ser números decimales. Las operaciones de elevar al cuadrado cada una de las desviaciones
no es un número entero, entonces las desviaciones suelen ser números decimales. Las operaciones de elevar al cuadrado cada una de las desviaciones![]() y multiplicarlas por las frecuencias respectivas pueden resultar sumamente laboriosas, por ello se suele usar otra fórmula en la que se evitan estos cálculos.
y multiplicarlas por las frecuencias respectivas pueden resultar sumamente laboriosas, por ello se suele usar otra fórmula en la que se evitan estos cálculos.
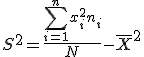
La desviación estándar o típica (S) se obtiene de la raíz cuadrada positiva de la varianza. Esta medida nos permite determinar el promedio aritmético de fluctuación de los datos respecto a su punto central o media. La desviación estándar nos da como resultado un valor numérico que representa la media de diferencia que hay entre los datos y la media. De su cálculo resulta por tanto un número más manejable, siendo este un parámetro más usado que la varianza.
![]()